こんにちは。今回は関数の極限について書いておきます。
関数の極限値の性質![]() ,
, ![]() のとき,
のとき, ![]()
![]()
![]()
![]() (複合同順)
(複合同順)![]()
![]()
![]()
![]()
![]()
※![]() が
が![]() だとしても, 関数
だとしても, 関数![]() の極限は考えられる。
の極限は考えられる。
![]() 極限値
極限値![]() に収束
に収束 ![]()
![]() 正の無限大に発散
正の無限大に発散 ![]()
![]() 負の無限大に発散
負の無限大に発散 ![]()
![]() 極限はない
極限はない
右側極限![]() と左側極限
と左側極限![]() がともに極限を持ちそれが一致することを言う。つまり,
がともに極限を持ちそれが一致することを言う。つまり, ![]()
【例】次の極限を調べよ。
(1) ![]()
(2) ![]()
(3) ![]()
(1) ![]() なので,
なので,
(与式)![]()
(2) 分子の有理化を行う。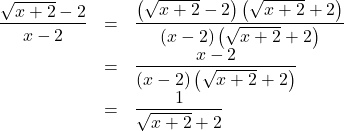
なので,
(与式)![]()
(3) ![]() が十分3に近いとき,
が十分3に近いとき, ![]() であり, 分子は15に近づき, 分母は0に近づくので,
であり, 分子は15に近づき, 分母は0に近づくので, ![]() の値は正の無限大に発散する。
の値は正の無限大に発散する。
したがって, ![]()
【例】関数![]() が次式で与えられるとき,
が次式で与えられるとき, ![]() ,
, ![]() を調べよ。
を調べよ。
(1) ![]()
(2) ![]()
(3) ![]()
(1) 分母分子を![]() で割る。
で割る。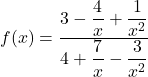 なので,
なので, ![]()
(2) 分母分子を![]() で割る。
で割る。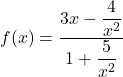 なので,
なので, ![]()
![]()
(3) 分子の有理化を行う。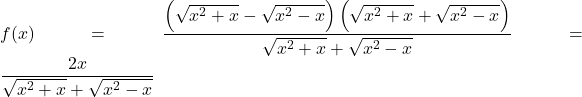
なので, 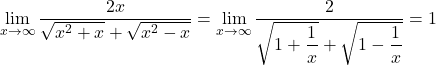
無理関数の![]() の極限を調べるとき, この場合は
の極限を調べるとき, この場合は![]() とおいてやる方がミスしにくい。
とおいてやる方がミスしにくい。
すると, ![]() が,
が, ![]() となり,
となり, ![]() なので,
なので, 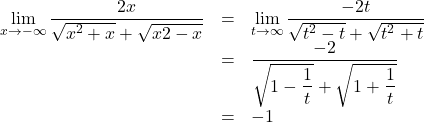
x→-無限大
![]() とおいて,
とおいて, ![]() ,
, ![]() として極限を調べるとよい。
として極限を調べるとよい。
【例】極限![]() を調べよ。
を調べよ。
![]() である。
である。
絶対値を外して考えるため, 絶対値の中の符号で場合分けする。![]() , つまり,
, つまり, ![]() のとき,
のとき, ![]() なので,
なので, ![]()
![]() , つまり,
, つまり, ![]() のとき,
のとき, ![]() なので,
なので, ![]()
となるので, ![]() は存在しない。
は存在しない。
 数樂管理人のブログ
数樂管理人のブログ 

