こんにちは。今回は定積分と不等式について書いておきます。
定積分の比較として次の関係が成り立ちます。
定積分の比較
![]()
![]() ならば,
ならば, ![]()
等号が成り立つのは, ![]()
![]() のときのみ
のときのみ
【例】![]() は3以上の自然数とする。
は3以上の自然数とする。
(1) ![]() のとき,
のとき, ![]() を証明せよ。
を証明せよ。
(2) ![]() を証明せよ。
を証明せよ。
【解答例】
(1) ![]() で,
で, ![]() は3以上の自然数であることから,
は3以上の自然数であることから, ![]() が成り立つ。この辺々に1を加えると,
が成り立つ。この辺々に1を加えると, ![]() となり, この逆数をとると,
となり, この逆数をとると, ![]()
となる。(証明終)
(2) (1)の等号は常には成り立たないので, 辺々を区間![]() で積分すると,
で積分すると, ![]()
となり, ![]()
また, ![]() で,
で, ![]() とおくと,
とおくと, 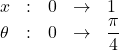
で, ![]() であるから,
であるから, 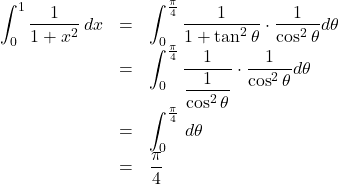
以上から, ![]()
が成り立つ。(証明終)
よく質問に挙がる「等号は常には成り立たないので」という意味は, ![]() で, 区間
で, 区間![]() において, 少しでも
において, 少しでも![]() となる区間があれば, 区間
となる区間があれば, 区間![]() で
で![]() と
と![]() を積分した(面積を求めた)場合, 計算結果は必ず
を積分した(面積を求めた)場合, 計算結果は必ず![]() の方(
の方(![]() の面積)が大きくなります。ですから, 積分計算時に等号がはずれるのです。
の面積)が大きくなります。ですから, 積分計算時に等号がはずれるのです。
 数樂管理人のブログ
数樂管理人のブログ 

