こんにちは。今回はグラフの漸近線について書いておきます。理屈を無視した感覚的な解法も載せておきますので, 一読ください。
漸近線の判定
関数![]() の曲線について
の曲線について
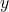 軸に垂直な漸近線
軸に垂直な漸近線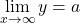 , または,
, または, 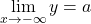 が成り立つとき, 直線
が成り立つとき, 直線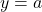 は漸近線になる。
は漸近線になる。 軸に垂直な漸近線
軸に垂直な漸近線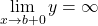 ,
, 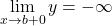 ,
, 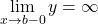 ,
, 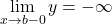 のいずれかが成り立つとき, 直線
のいずれかが成り立つとき, 直線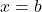 は漸近線になる。
は漸近線になる。 軸に垂直でない漸近線
軸に垂直でない漸近線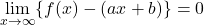 であるならば, 直線
であるならば, 直線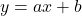 は漸近線になる。
は漸近線になる。 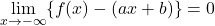 についても同様。
についても同様。
また,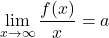 ,
, 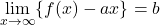 ならば,
ならば, 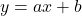 が漸近線になる。
が漸近線になる。
【例】次の曲線の漸近線の方程式を求めよ。![]()
【解答例】![]() と変形できる。
と変形できる。
これの分数の項に着目して, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
であるから, ![]() ,
, ![]() は漸近線になる。
は漸近線になる。
また, 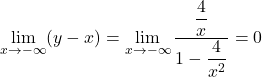 ,
, 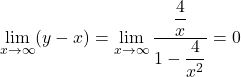
なので, ![]() は漸近線になる。
は漸近線になる。
以上より漸近線は, ![]() ,
, ![]()
【理屈を無視するとこう考えられる】
結局, 漸近線はこの値になると困るという値だったり, 一方が0に近づいたとき残った片方が漸近線であったりします。この問題の場合, 分母が0になったら困るので, 分母が0になる値である![]() が漸近線になります。また,
が漸近線になります。また, ![]() は,
は, ![]() の分母が大きくなって0に近づけば,
の分母が大きくなって0に近づけば, ![]() が残って, それに近づいていくので,
が残って, それに近づいていくので, ![]() が漸近線になります。感覚的なものですが, つかんでおくと便利です。
が漸近線になります。感覚的なものですが, つかんでおくと便利です。
【例】関数![]() の増減, グラフの凹凸, 漸近線を調べて, グラフを描け。
の増減, グラフの凹凸, 漸近線を調べて, グラフを描け。
【解答例】
![]()
![]() よって
よって![]() となる点はない。
となる点はない。
つまり, 変曲点はない。![]() となる点は,
となる点は, ![]() より
より![]() のときであり,
のときであり, ![]() の増減, グラフの凹凸は次のようになる。
の増減, グラフの凹凸は次のようになる。
また, ![]() ,
, ![]() であるから, 漸近線の1つは
であるから, 漸近線の1つは![]() 軸である。
軸である。
さらに, ![]()
![]()
であるから, もう1つの漸近線は![]() である。
である。
以上よりグラフは以下のようになる。
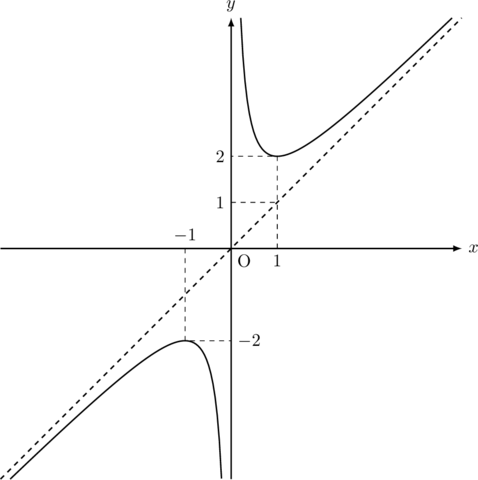
【理屈を無視するとこう考えられる】
上の問題同様, これも
 数樂管理人のブログ
数樂管理人のブログ