今回は関数の増減, 極値について書いておきます。
【増加関数】
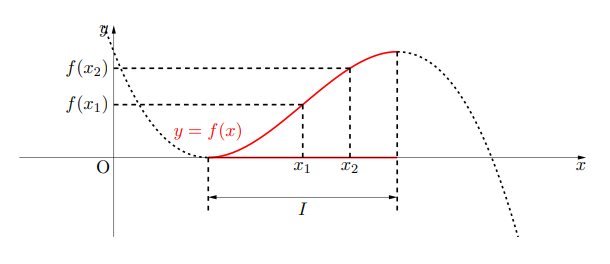
区間![]() で定義された関数
で定義された関数![]() が,
が, ![]() に属する任意の
に属する任意の![]() の値
の値![]() ,
, ![]() に対し,
に対し, ![]()
が成り立つとき, グラフは右上がりになり, 関数![]() は区間
は区間![]() で増加(単調に増加)するという。このような関数を増加関数という。
で増加(単調に増加)するという。このような関数を増加関数という。
【減少関数】
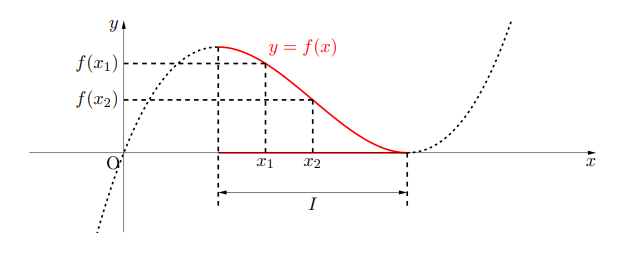
区間![]() で定義された関数
で定義された関数![]() が,
が, ![]() に属する任意の
に属する任意の![]() の値
の値![]() ,
, ![]() に対し,
に対し, ![]()
が成り立つとき, グラフは右下がりになり, 関数![]() は区間
は区間![]() で減少(単調に減少)するという。このような関数を減少関数という。
で減少(単調に減少)するという。このような関数を減少関数という。
【定数関数】
区間![]() で定義された関数
で定義された関数![]() が,
が, ![]() に属する任意の
に属する任意の![]() に対し, 常に一定の値
に対し, 常に一定の値![]() をとる。すなわち,
をとる。すなわち, ![]() であるとき, 関数
であるとき, 関数![]() は区間
は区間![]() で定数であるという。このような関数を定数関数という。
で定数であるという。このような関数を定数関数という。
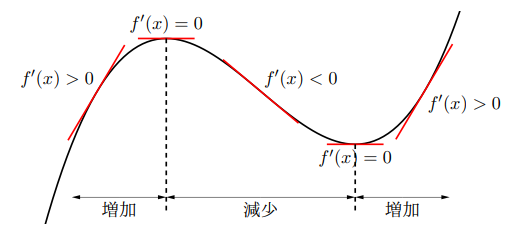
関数![]() が
が![]() で連続,
で連続, ![]() で微分可能なとき,
で微分可能なとき, ![]()
![]() で
で![]() ならば,
ならば, ![]() は
は![]() で増加
で増加![]()
![]() で
で![]() ならば,
ならば, ![]() は
は![]() で減少
で減少
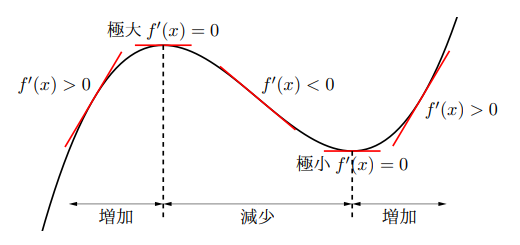
関数![]() が
が![]() を境目に増加から減少に変わるとき,
を境目に増加から減少に変わるとき, ![]() は
は![]() で極大であるといい,
で極大であるといい, ![]() を関数
を関数![]() の極大値という。また, 関数
の極大値という。また, 関数![]() が
が![]() を境目に減少から増加に変わるとき,
を境目に減少から増加に変わるとき, ![]() は
は![]() で極小であるといい,
で極小であるといい, ![]() を関数
を関数![]() の極小値という。また, 極大値と極小値をまとめて極値という。
の極小値という。また, 極大値と極小値をまとめて極値という。
 数樂管理人のブログ
数樂管理人のブログ