こんにちは。今回は数学的帰納法の問題をやってみます。それでは早速いってみましょう。
【問題】不等式![]()
が成り立つことを数学的帰納法によって証明せよ。
【解答例】![]() のとき, (左辺)
のとき, (左辺)![]() , (右辺)
, (右辺)![]() で等式が成立
で等式が成立![]() のとき,
のとき, ![]()
が成り立つと仮定すると, ![]() のとき,
のとき, ![]()
となり, ![]() の右辺と,
の右辺と, ![]() の大小関係を調べると,
の大小関係を調べると, 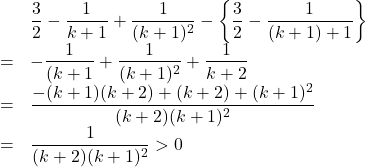
したがって, この結果と![]() より,
より, ![]()
となり, ![]() のときも成り立つ。
のときも成り立つ。
したがってすべての自然数![]() において題の不等式は成り立つ。
において題の不等式は成り立つ。
こんにちは。今回は数学的帰納法の問題をやってみます。それでは早速いってみましょう。
【問題】不等式![]()
が成り立つことを数学的帰納法によって証明せよ。
【解答例】![]() のとき, (左辺)
のとき, (左辺)![]() , (右辺)
, (右辺)![]() で等式が成立
で等式が成立![]() のとき,
のとき, ![]()
が成り立つと仮定すると, ![]() のとき,
のとき, ![]()
となり, ![]() の右辺と,
の右辺と, ![]() の大小関係を調べると,
の大小関係を調べると, 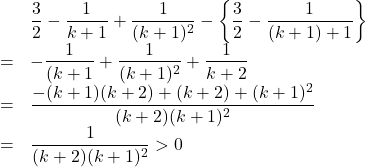
したがって, この結果と![]() より,
より, ![]()
となり, ![]() のときも成り立つ。
のときも成り立つ。
したがってすべての自然数![]() において題の不等式は成り立つ。
において題の不等式は成り立つ。