こんにちは。今回は数IIIの回転体の体積を求めるのに有効な技である。バウムクーヘン積分法の紹介です。![]() 軸について回転するときに威力を発揮する公式です。それでは見ていきましょう。
軸について回転するときに威力を発揮する公式です。それでは見ていきましょう。
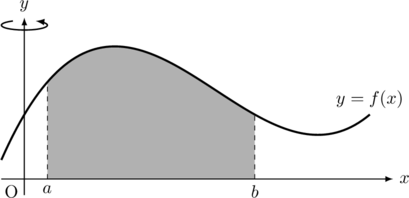
バウムクーヘン積分法の公式
関数![]() ,
, ![]() 軸,
軸, ![]() ,
, ![]() に囲まれる領域を
に囲まれる領域を![]() 軸について回転させたときにできる回転体の体積
軸について回転させたときにできる回転体の体積![]() は,
は,![]()
で与えられる。
これが, バウムクーヘン積分法の公式である。
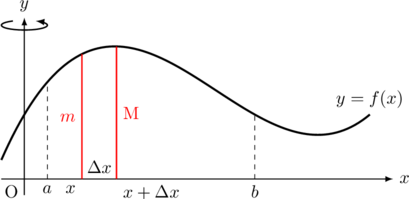
今, 区間![]() 内の
内の![]() から
から![]() (赤の区間)を回転させることを考える。また,
(赤の区間)を回転させることを考える。また, ![]() ,
, ![]() とする。
とする。
このとき, イメージとしては以下のような感じになる。

このとき. 赤の区間を回転させたときにできる立体の内側の高さ
辺々
ここで,
となり, はさみうちの原理より,
なので,
体積を
よって, 求める体積
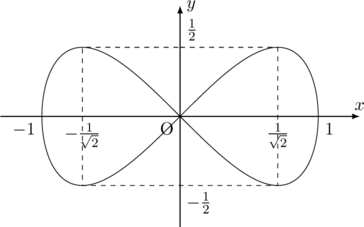
【例】曲線![]() を,
を, ![]() 軸の回りに回転させてできる立体の体積を求めよ。
軸の回りに回転させてできる立体の体積を求めよ。
【解答例】
与えられた関数を![]() について解くと,
について解くと, ![]() これをもとにグラフを描くと, 以下のような感じになります。これを
これをもとにグラフを描くと, 以下のような感じになります。これを![]() 軸について回転させることを考える。
軸について回転させることを考える。
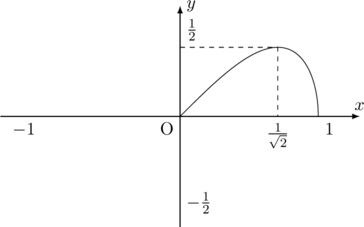
このとき, 以下の部分だけ回転させて, 上下分で2倍すればよいことになります。
したがって, 求める体積
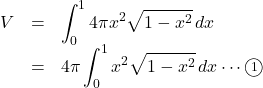
ここで,
![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle \int_0^1 x^2\sqrt{1-x^2}\,dx&=&\displaystyle \int_0^\frac{\pi}{2} \sin^2\theta\cos\theta\cdot\cos\theta\,d\theta\\&=&\displaystyle \int_0^\frac{\pi}{2}\left(\sin\theta\cos\theta\right)^2\, d\theta\\&=&\displaystyle \int_0^\frac{\pi}{2}\left(\dfrac12\sin2\theta\right)^2\, d\theta\\&=&\displaystyle \int_0^\frac{\pi}{2}\dfrac{1}{4}\cdot\dfrac{1-\cos4\theta}{2}\, d\theta\\&=&\dfrac{1}{8}\left[\theta-\dfrac14\sin4\theta\right]_0^{\frac{\pi}{2}}\\&=&\dfrac18\cdot\dfrac{\pi}{2}\\&=&\dfrac{\pi}{16}\cdots\maru2\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-1b6066f0d67576ff5da1f84e2f485a78_l3.png)
よって
この曲線はリサージュ曲線と呼ばれる曲線であるようです。
では。
この裏技公式ですが, 使っていいという解釈とそうでないという解釈があります。個人的には受験生は現役生だけではないので, 何のテクニックを使ってもいいと思います。したがって, この裏技も本番で使っていいというのが私の見解です。もちろん, 証明をすれば堂々と使えるのは確かなのですが,証明をしていたのでは時短になりません。使う本人が不安なのであれば, 使用はやめたほうが無難でしょう。私は問題ないと思いますけどね。ただし, 個人の感想ですので, 減点に関しては責任を負いかねます。その点よろしくお願いします。
 数樂管理人のブログ
数樂管理人のブログ 

