emath：中学数学：平行四辺形と面積比(公式編)

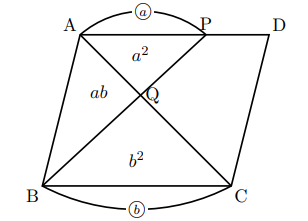
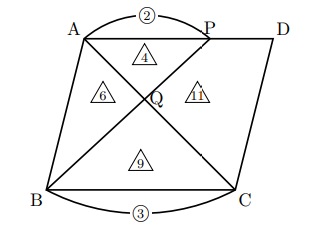
こんにちは。平行四辺形と面積の問題でこういった問題を瞬間的に解法していく公式を紹介します。
まず, 例題を見ていこう。

例題

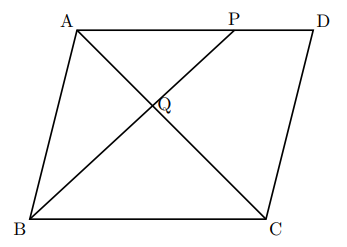
上の図で, 右の図で四角形ABCDは平行四辺形で, Pは辺ADを2 : 1に分ける点である。線分PBと線分ACの交点をQとするとき, 次の問いに答えなさい。
(1) 四角形PQCDの面積と平行四辺形ABCDの面積の比を最も簡単な整数の比で表しなさい。

公式の存在

こういった図形には面積の割合を表す公式が存在します。それが以下の図です。

△AQP∽△CQBで, $\mathrm{AP} : \mathrm{CB} = \maru{a} : \maru{b}$ なら, 相似比と面積比の関係から, △APQ $=a^2$ , △CBQ $=b^2$ , △ABQ $=ab$ となります。
これで, 平行四辺形の面積の半分である, △ABCが $b^2+ab$ となるので, 四角形PQCDの面積の割合は, $b^2+ab-a^2$ となります。
【補足】△ABQが $ab$ で表されるのは, $\mathrm{AQ} : \mathrm{CQ}= a : b$ で, △CBQが $b^2$ なので, △ABQを $x$ とおくと, $a : b = x : b^2$ として, $x=ab$ が得られるからであります。

公式を使って解法してみる

上の図で, AP : CB $=2 : 3$ (△AQP∽△CQB)であるから, △AQP : △CQB $=$ :
△AQBは, PQ : QB $=2 : 3$ (△AQP∽△CQB)より, $2\times3=$
これで平行四辺形の面積の半分(△ABC)がであるから, 四角形PQCD $=$ (△ADC) $-$ (△AQP) $=$
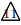
よって, 四角形PQCDの面積と平行四辺形ABCDの面積の比は
$11 : 30$
である。