こんにちは。メネラウスの定理を使う問題をやってみましょう。それではどうぞ。
![]() において, 辺
において, 辺![]() を3等分する点を
を3等分する点を![]() に近い方から順に
に近い方から順に![]() とする。さらに, 辺
とする。さらに, 辺![]() を
を![]() に内分する点を
に内分する点を![]() , 線分
, 線分![]() と線分
と線分![]() の交点を
の交点を![]() , 線分
, 線分![]() の延長線と辺
の延長線と辺![]() との交点を
との交点を![]() とする。このとき, 次の問いに答よ。
とする。このとき, 次の問いに答よ。
(1) ![]() の比を求めよ。
の比を求めよ。
(2) ![]() の比を求めよ。
の比を求めよ。
(3) ![]() の比を求めよ。
の比を求めよ。
(4) ![]() の面積を
の面積を![]() とするとき,
とするとき, ![]() の面積を
の面積を![]() を用いて表せ。
を用いて表せ。
【解答例】
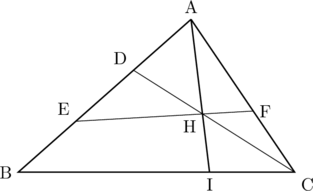
(1) △ADCと線分AEで, メネラウスの定理より,
よって,
(2) △BCDと線分AIで, メネラウスの定理より,
よって,
(3) △ABIと線分CDで, メネラウスの定理より,
(4)
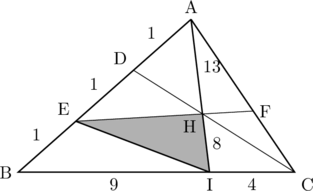
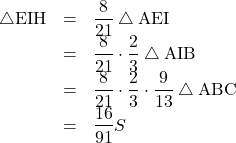
よって,
 数樂管理人のブログ
数樂管理人のブログ 


