こんにちは。早速やって行きまでょう。
変量![]() の各データ(データ数10)を2倍して4を加えて得られる変量を
の各データ(データ数10)を2倍して4を加えて得られる変量を![]() , 変量
, 変量![]() の各データ(データ数10)の値に10を加えて得られる変量を
の各データ(データ数10)の値に10を加えて得られる変量を![]() とする。このとき, 次の問いに答よ。
とする。このとき, 次の問いに答よ。
(1) 変量![]() の分散は変量
の分散は変量![]() の分散の何倍か。
の分散の何倍か。
(2) 変量![]() の分散は変量
の分散は変量![]() の分散の何倍か。
の分散の何倍か。
(3) 変量![]() と変量
と変量![]() の共分散は, 変量
の共分散は, 変量![]() と変量
と変量![]() の共分散の何倍か。
の共分散の何倍か。
(4) 変量![]() と変量
と変量![]() の相関係数は, 変量
の相関係数は, 変量![]() と変量
と変量![]() の相関係数の何倍か。
の相関係数の何倍か。
【解答例】
以下, ![]() は10以下の自然数, 変量
は10以下の自然数, 変量![]() の標準偏差を
の標準偏差を![]() とし, 変量
とし, 変量![]() の共分散
の共分散![]() , 変量
, 変量![]() の共分散を
の共分散を![]() とします。
とします。
(1) ![]() だから,
だから, ![]()
4倍![]() (答)
(答)
(2) ![]() だから,
だから, ![]()
1倍![]() (答)
(答)
(3) ![]()
2倍![]() (答)
(答)
(3) 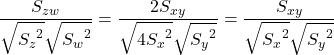
1倍![]() (答)
(答)
※このことは, 変量![]() のデータ数がそれぞれ
のデータ数がそれぞれ![]() (
(![]() は任意の自然数)の場合でも成り立つ。
は任意の自然数)の場合でも成り立つ。
 数樂管理人のブログ
数樂管理人のブログ 


