こんにちは。今回は定期テストや実力テストによく出題される問題をやってみましょう。それではどうぞ。
【問題】![]() において,
において, ![]() が成り立っている。次の問いに答えよ。
が成り立っている。次の問いに答えよ。
(1) この三角形で最も大きい角の大きさを求めよ。
(2) ![]() の大きさは
の大きさは![]() より大きいことを示せ。
より大きいことを示せ。
【解答例】
正弦定理![]()
より, ![]() が成り立つ。
が成り立つ。
問題より, ![]() であるから,
であるから, ![]() であり,
であり, ![]() (
(![]() )とおける。
)とおける。
最大辺は![]() であるから, 最大角は
であるから, 最大角は![]() であるので, 余弦定理を用いると,
であるので, 余弦定理を用いると, 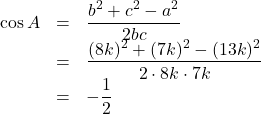
よって, 最大角は![]()
(2) 余弦定理を用いると, 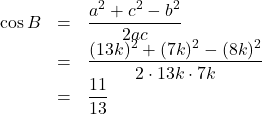
ここで, ![]() で,
で, ![]() が
が![]() より大きいことを示すには,
より大きいことを示すには, ![]() を示せばよい。
を示せばよい。
そこで, ![]() と
と![]() を通分すると,
を通分すると,
それぞれ, ![]() となり,
となり,
分子の![]() と
と![]() をそれぞれ2乗して, 大小関係を比較すると
をそれぞれ2乗して, 大小関係を比較すると![]() ,
, ![]()
となり, ![]() となる。
となる。
したがって, ![]()
である。
押さえておくべきポイント
![]() 正弦定理
正弦定理![]() から,
から, ![]()
![]()
![]()
が得られ, ![]() が得られる。
が得られる。![]()
![]() を示すには, 余弦定理などを用いて,
を示すには, 余弦定理などを用いて, ![]() を示せばよい。
を示せばよい。
これは, ![]() の値が
の値が![]() から角度が大きくなるにつれて, だんだんと小さくなっていく性質を用いている。
から角度が大きくなるにつれて, だんだんと小さくなっていく性質を用いている。
 数樂管理人のブログ
数樂管理人のブログ 


