TikZ：中学数学：R5(2023)年度徳島県公立高校入試：数学：大問5　空間図形

こんにちは。受験生の皆さんお疲れ様です。早速問題をみていきましょう。

空間図形

【問題】下の図のように, すべての辺の長さが $6\,$ cmの正三角錐OABCがある。辺OB上に点Dをとり, 辺BC上の点をMとする。 $\mathrm{OD}=4\,$ cmのとき, (1)～(4)に答えなさい。

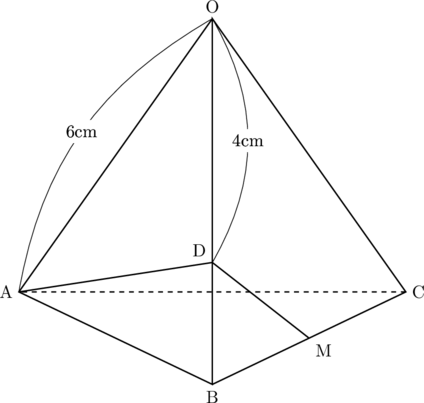
(1) 正三角錐OABCで, 辺ABとねじれの位置にある辺はどれか, 書きなさい。
(2) △OAD∽△BMDを証明しなさい。
(3) $\mathrm{AD}+\mathrm{DM}$ の長さを求めなさい。
(4) 辺OC上に点Pをとる。4点O, A, D, Pを頂点とする立体OADPの体積が正三角錐OABC体積の $\dfrac27$ 倍であるとき, 線分OPの長さを求めなさい。

解答

【略解】詳細解は下部にリンクあり。関連公式はその下部にあり。
(1) 辺OC
(2)
△OADと△BMDで,
仮定より,
$\mathrm{OA : BM} = 6 : 3 = 2 : 1\cdots\maru1$
$\mathrm{OD : BD} = 4 : 2 = 2 : 1\cdots\maru2$
△OAB, △OBCは正三角形なので,
$\kaku{AOD}=\kaku{BMD}=60\Deg\cdots\maru3$
$\maru1, \maru2, \maru3$ より,
2組の辺の比とその間の角がそれぞれ等しいので,
△OAD∽△BMD
(3)
(2)より, $\mathrm{AD}, \mathrm{DM}$ は一直線に並ぶので, 線分AMを斜辺とする直角三角形をつくり, 三平方の定理から,
$\mathrm{AM}=\sqrt{\left(\dfrac{15}{2}\right)^2+\left(\dfrac{3\sqrt3}{2}\right)^2}=3\sqrt7$
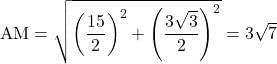
$3\sqrt7\,$ cm
(4)
三角錐の体積比の公式を用いて,
$\dfrac{6}{6}\times\dfrac46\times\dfrac{a}{6}=\dfrac27$
となり, これを解いて,
$\dfrac{18}{7}\,$ cm