こんにちは。今回は![]() の微分についてです。対数微分法を用いると楽なのでそれで証明しましょう。以下,
の微分についてです。対数微分法を用いると楽なのでそれで証明しましょう。以下, ![]() として進めていきます。
として進めていきます。
![]() を
を![]() として, 両辺の対数をとると,
として, 両辺の対数をとると, ![]() となり,
となり, ![]() となる。
となる。
これを![]() について微分すると,
について微分すると, ![]()
![]()
よって, ![]()
以上になります。
他の方法を挙げると, ![]() とおいて,
とおいて,
両辺の対数をとると, ![]() なる。ここから,
なる。ここから, ![]() として,
として,
両辺を![]() で微分すると,
で微分すると, 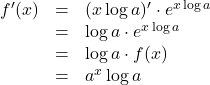
よって, ![]()
以上になります。
こんにちは。今回は![]() の微分についてです。対数微分法を用いると楽なのでそれで証明しましょう。以下,
の微分についてです。対数微分法を用いると楽なのでそれで証明しましょう。以下, ![]() として進めていきます。
として進めていきます。
![]() を
を![]() として, 両辺の対数をとると,
として, 両辺の対数をとると, ![]() となり,
となり, ![]() となる。
となる。
これを![]() について微分すると,
について微分すると, ![]()
![]()
よって, ![]()
以上になります。
他の方法を挙げると, ![]() とおいて,
とおいて,
両辺の対数をとると, ![]() なる。ここから,
なる。ここから, ![]() として,
として,
両辺を![]() で微分すると,
で微分すると, 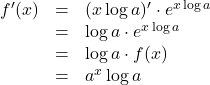
よって, ![]()
以上になります。