こんにちは。今回は商の微分について書いておきます。なんであの公式なんでしょう。その証明を書いておきます。
商の微分の公式
商の微分の公式とは以下のものを表す。![]() についての関数
についての関数![]() を
を![]() について微分すると,
について微分すると, ![]()
となる。
証明は導関数の定義にしたがって行われます。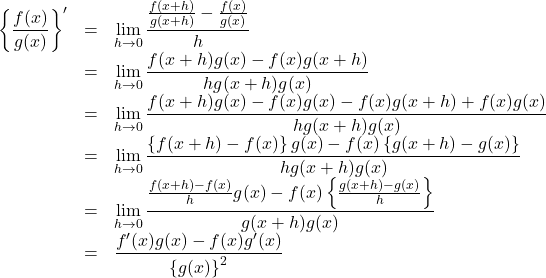
よって, ![]()
となる。
【証明のコツ】
2行目から3行目の変形では, 分子に![]() を追加しており, 4行目から5行目へと変形するときに, 導関数の定義が使えるように分母分子を
を追加しており, 4行目から5行目へと変形するときに, 導関数の定義が使えるように分母分子を![]() で割っている。
で割っている。
こんにちは。今回は商の微分について書いておきます。なんであの公式なんでしょう。その証明を書いておきます。
商の微分の公式とは以下のものを表す。![]() についての関数
についての関数![]() を
を![]() について微分すると,
について微分すると, ![]()
となる。
証明は導関数の定義にしたがって行われます。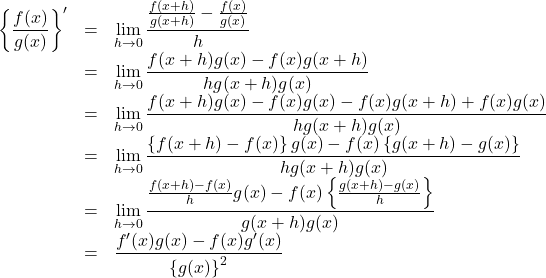
よって, ![]()
となる。
【証明のコツ】
2行目から3行目の変形では, 分子に![]() を追加しており, 4行目から5行目へと変形するときに, 導関数の定義が使えるように分母分子を
を追加しており, 4行目から5行目へと変形するときに, 導関数の定義が使えるように分母分子を![]() で割っている。
で割っている。