こんにちは。今回は![]() の微分について書いておきます。導関数の定義にしたがって微分していきましょう。
の微分について書いておきます。導関数の定義にしたがって微分していきましょう。
公式
![]() を
を![]() について微分すると,
について微分すると, ![]()
となる。
導関数の定義にしたがって微分すると, ![]()
これだけ見ると, ![]() ってどうやって計算するんですかってなるけど, ここで使うテクニックが二項定理。
ってどうやって計算するんですかってなるけど, ここで使うテクニックが二項定理。![]() を二項定理を用いて展開すると,
を二項定理を用いて展開すると, ![]()
![]() を
を![]() に代入すると,
に代入すると, 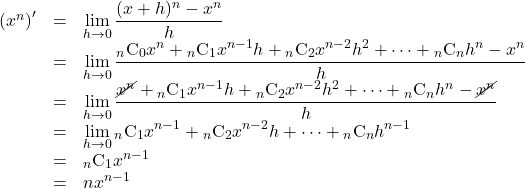
となる。
よって, ![]()
![]() とする。
とする。![]() とおいて, 両辺の対数をとると,
とおいて, 両辺の対数をとると, ![]() となる。
となる。
つまり, ![]() となり, この両辺を
となり, この両辺を![]() で微分すると,
で微分すると, ![]()
![]()
![]() なので,
なので, ![]()
よって, ![]()
こんにちは。今回は![]() の微分について書いておきます。導関数の定義にしたがって微分していきましょう。
の微分について書いておきます。導関数の定義にしたがって微分していきましょう。
![]() を
を![]() について微分すると,
について微分すると, ![]()
となる。
導関数の定義にしたがって微分すると, ![]()
これだけ見ると, ![]() ってどうやって計算するんですかってなるけど, ここで使うテクニックが二項定理。
ってどうやって計算するんですかってなるけど, ここで使うテクニックが二項定理。![]() を二項定理を用いて展開すると,
を二項定理を用いて展開すると, ![]()
![]() を
を![]() に代入すると,
に代入すると, 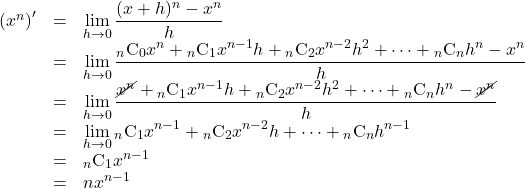
となる。
よって, ![]()
![]() とする。
とする。![]() とおいて, 両辺の対数をとると,
とおいて, 両辺の対数をとると, ![]() となる。
となる。
つまり, ![]() となり, この両辺を
となり, この両辺を![]() で微分すると,
で微分すると, ![]()
![]()
![]() なので,
なので, ![]()
よって, ![]()