こんにちは。今回はカテナリー曲線とその類似関数のグラフの特徴を示しておきます。頻出系の関数ですので, グラフの概形など覚えておきましょう。後に補足として, カテナリー曲線の長さと面積の性質を記しておきます。
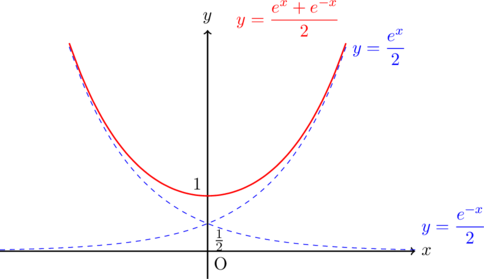
![]() カテナリー
カテナリー![]() とおくと,
とおくと, ![]()
![]()
![]() となるのは,
となるのは, ![]() のとき, このときこの曲線は極小値をとり, その値は
のとき, このときこの曲線は極小値をとり, その値は![]() 。
。
極大値はない。
変曲点は![]() より, 存在しない。
より, 存在しない。
グラフの漸近線(曲線)は![]() のとき,
のとき, ![]() ,
, ![]() のとき,
のとき, ![]() となる。
となる。
これは, ![]() で,
で, ![]() のとき,
のとき, ![]() となるので,
となるので, ![]() は
は![]() に近づき,
に近づき, ![]() で,
で, ![]() のとき,
のとき, ![]() となるので,
となるので, ![]() は
は![]() に近づくことからわかる。
に近づくことからわかる。
ちなみに,
![]()
![]() とおくと,
とおくと, ![]()
![]()
![]() より,
より, ![]() は単調増加の関数である。よって, 極値は存在しない。
は単調増加の関数である。よって, 極値は存在しない。![]() とすると,
とすると, ![]() なので, 変曲点は
なので, 変曲点は![]() になる。
になる。
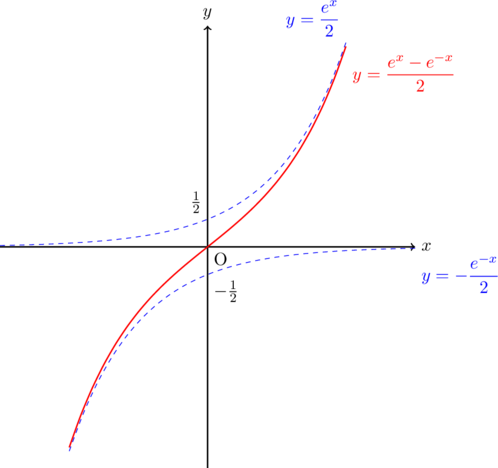
グラフの漸近線(曲線)は![]() のとき,
のとき, ![]() ,
, ![]() のとき,
のとき, ![]() となる。
となる。
これは, ![]() で,
で, ![]() のとき,
のとき, ![]() となるので,
となるので, ![]() は
は![]() に近づき,
に近づき, ![]() で,
で, ![]() のとき,
のとき, ![]() となるので,
となるので, ![]() は
は![]() に近づくことからわかる。
に近づくことからわかる。
ちなみに,
カテナリー曲線の性質として, ある区間の曲線の長さ![]() は, その区間の面積
は, その区間の面積![]() に比例するというものがあります。
に比例するというものがあります。
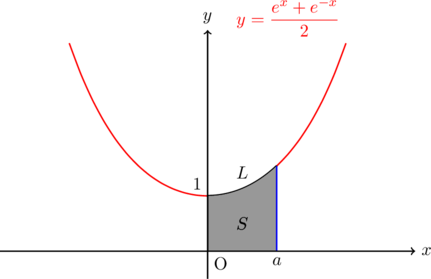
実際に積分区間を
これより,
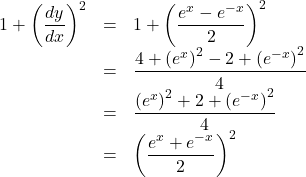
よって,
![Rendered by QuickLaTeX.com \begin{array}{lll}L&=&\displaystyle\int_0^a\sqrt{1+\left(\dfrac{dy}{dx}\right)^2}\, dx\\.&=&\displaystyle\int_0^a\sqrt{\left(\dfrac{e^x+e^{-x}}{2}\right)^2}\, dx\\&=&\displaystyle\int_0^a\dfrac{e^x+e^{-x}}{2}\, dx\\&=&\left[\dfrac{e^x-e^{-x}}{2}\right]_0^a\\&=&\dfrac{e^a-e^{-a}}{2}\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-4885299b3db2a7c54690f12bb09ecdbf_l3.png)
ここで, 面積
このことから,
 数樂管理人のブログ
数樂管理人のブログ 

