こんにちは。これもよく登場する![]() 平面上の傾きのある直線を軸とする回転体の求め方の話です。先ずは例題を解きながら見ていきましょう。
平面上の傾きのある直線を軸とする回転体の求め方の話です。先ずは例題を解きながら見ていきましょう。
【例題】放物線![]() と直線
と直線![]() で囲まれた図形を, 直線
で囲まれた図形を, 直線![]() を軸として1回転させてできる立体の体積を求めよ。
を軸として1回転させてできる立体の体積を求めよ。
図示すると以下のようになる。
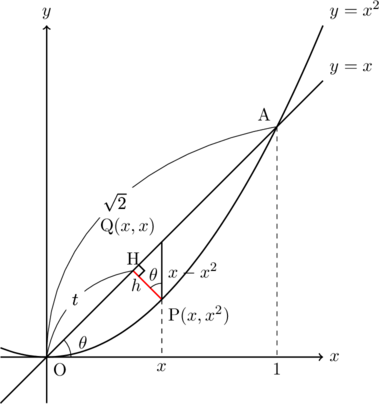
今回図中の![]() (直線
(直線![]() と
と![]() 軸とのなす角)は
軸とのなす角)は![]() で, Pは放物線上の点, Qは
で, Pは放物線上の点, Qは![]() 上の点で,
上の点で, ![]() 座標は等しい。
座標は等しい。![]() ,
, ![]() とする。このとき, 線分
とする。このとき, 線分![]() (
(![]() )を直線
)を直線![]() を軸として1回転してできる円の面積を
を軸として1回転してできる円の面積を![]() にそって線分
にそって線分![]() の区間で積分することを考える。
の区間で積分することを考える。![]() とすると, 求める体積
とすると, 求める体積![]() は,
は, ![]()
と表せる。
ここで, ![]() を求めると,
を求めると, ![]() ,
, ![]() なので,
なので, ![]()
![]() であり,
であり, ![]() ,
, ![]() であるから,
であるから, ![]()
この![]() を
を![]() で微分すると,
で微分すると, ![]()
となる。![]() より,
より, ![]() を計算すると,
を計算すると, ![Rendered by QuickLaTeX.com \begin{array}{lll}V&=&\pi\displaystyle\int_0^{\sqrt2}h^2\ dt\\&=&\pi\displaystyle\int_0^1\left(\dfrac{x-x^2}{\sqrt2}\right)^2\dfrac{1+2x}{\sqrt2}\ dx\\&=&\dfrac{\pi}{2\sqrt2}\displaystyle\int_0^1(x^2-3x^4+2x^5)\ dx\\&=&\dfrac{\pi}{2\sqrt2}\left[\dfrac13x^3-\dfrac35x^5+\dfrac13x^6\right]_0^1\\&=&\dfrac{\pi}{30\sqrt2}\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-8554049658af6280a30645abb83538ea_l3.png)
となる。
関数![]() と直線
と直線![]() によって囲まれる面積を, 直線
によって囲まれる面積を, 直線![]() について1回転させてできる立体の体積を求めてみる。2つのグラフの交点の
について1回転させてできる立体の体積を求めてみる。2つのグラフの交点の![]() 座標は
座標は![]() とする。
とする。
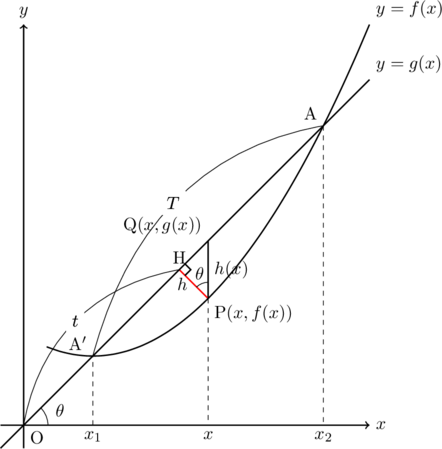
直線
と表せる。
ここで,
この
となる。
![Rendered by QuickLaTeX.com \begin{array}{lll}V&=&\pi\displaystyle\int_{x_1}^{x_1+T}h^2\ dt\\&=&\pi\displaystyle\int_{x_1}^{x_2}\left\{h(x)\cos\theta\right\}^2\left\{\dfrac{1}{\cos\theta}-h'(x)\sin\theta\right\}\ dx\\&=&\pi\displaystyle\int_{x_1}^{x_2}\left\{(h(x))^2\cos\theta-(h(x))^2 h'(x)\sin\theta\cos^2\theta\right\}\ dx\\&=&\pi\cos\theta\displaystyle\int_{x_1}^{x_2}\left\{h(x)\right\}^2\ dx-\pi\sin\theta\cos^2\theta\displaystyle\int_{x_1}^{x_2}\left\{h(x)\right\}^2h'(x)\ dx\\&=&\pi\cos\theta\displaystyle\int_{x_1}^{x_2}\left\{h(x)\right\}^2\ dx-\pi\sin\theta\cos^2\theta\left[\dfrac{\left\{h(x)\right\}^3}{3}\right]_{x_1}^{x_2}\cdots\textcircled{\scriptsize 4}\\&=&\pi\cos\theta\displaystyle\int_{x_1}^{x_2}\left\{h(x)\right\}^2\ dx\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-606202679a16f66128f18b45e242545c_l3.png)
となる。
よって, 求める体積は
で与えられる。
ちなみに
![Rendered by QuickLaTeX.com \left[\dfrac{\left\{h(x)\right\}^3}{3}\right]_{x_1}^{x_2}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-10ae83e0d340806d60fbe9865491bcc1_l3.png) の計算であるが,
の計算であるが, また, 関数
とすることで, 同じ結果が得られる。
 数樂管理人のブログ
数樂管理人のブログ 

