こんにちは。今回は三角関数の関数で, 合成を用いる場合の最大値・最小値を見ていきましょう。それではどうぞ。
【例題】![]() のとき, 関数
のとき, 関数![]() の最大値と最小値を求めよ。また, そのときの
の最大値と最小値を求めよ。また, そのときの![]() の値を求めよ。
の値を求めよ。
【方針】
方針としては, ![]() または
または![]() のみで関数を表せそうにないことに着目。理由は
のみで関数を表せそうにないことに着目。理由は![]() の項があるから。したがって,
の項があるから。したがって, ![]() とおいて, 両辺2乗して話を進めるか,
とおいて, 両辺2乗して話を進めるか, ![]() なので, それを用いて, 三角関数の合成に持ち込むかの2択になりそうである。
なので, それを用いて, 三角関数の合成に持ち込むかの2択になりそうである。![]() とおいた場合,
とおいた場合, ![]() ,
, ![]() の処理が困るので, 選択肢としては不適となる。したがって,
の処理が困るので, 選択肢としては不適となる。したがって, ![]() ,
, ![]() ,
, ![]() を用いて, 三角関数の合成に持ち込む。
を用いて, 三角関数の合成に持ち込む。
【解答例】![]() ,
, ![]() ,
, ![]() より,
より, 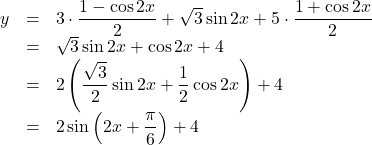
![]() より,
より, ![]() だから,
だから, ![]() は,
は, ![]() で最大値
で最大値![]()
![]() で最小値
で最小値![]()
をとる。
よって, ![]() で最大値6,
で最大値6, ![]() で最小値2
で最小値2
となる。
 数樂管理人のブログ
数樂管理人のブログ 

