こんにちは。群数列の問題をやってみましょう。
【問題】![]() ,
, ![]() で定められる数列
で定められる数列![]() を次のような群に分ける。このとき, 以下の問いに答えなさい。
を次のような群に分ける。このとき, 以下の問いに答えなさい。![]()
ただし, ![]() は第1群,
は第1群, ![]() ~
~![]() は第2群,
は第2群, ![]() ~
~![]() は第3群,
は第3群, ![]() ~
~![]() は第4群,
は第4群, ![]() は第5群,
は第5群, ![]() とします。
とします。
(1) 第10群に含まれる項の個数を答えなさい。
(2) 数列![]() の一般項を求めなさい。
の一般項を求めなさい。
(3) ![]() となる項
となる項![]() は第何群に含まれているか求めなさい。
は第何群に含まれているか求めなさい。
(4) 第![]() 群の最初の数を
群の最初の数を![]() を用いて表しなさい。
を用いて表しなさい。
【福島大改題】
【解答例】
(1) ![]() 群の項の個数は
群の項の個数は![]() (個)なので,
(個)なので, ![]() より, 19個
より, 19個![]() (答)
(答)
(2) ![]() は,
は, ![]() と変形できるので,
と変形できるので, ![]() を求めると,
を求めると, ![]() 。したがって,
。したがって, ![]() となり,
となり,
数列![]() は初項
は初項![]() 公比
公比![]() の等比数列なので,
の等比数列なので, ![]()
よって, ![]() (答)
(答)
(3) ![]()
![]()
![]()
![]() より,
より, ![]()
第11項は第4群なので, 第4群![]() (答)
(答)
(4) ![]() とすると,
とすると, ![]() 群の最初の数の項の番号
群の最初の数の項の番号![]() は,
は, ![]() 群までの項の個数の和に1を加えたものだから,,
群までの項の個数の和に1を加えたものだから,, 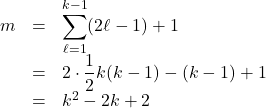
これは![]() のときも成り立つ。
のときも成り立つ。
よって, ![]() 群の最初の数は,
群の最初の数は, ![]()
![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ 


