受験算数：図形：重なりのある面積(筑波大学附属中)

2023年8月10日

こんにちは。問題文中少し表現を変更しています。それではどうぞ。

2019筑波大学附属中

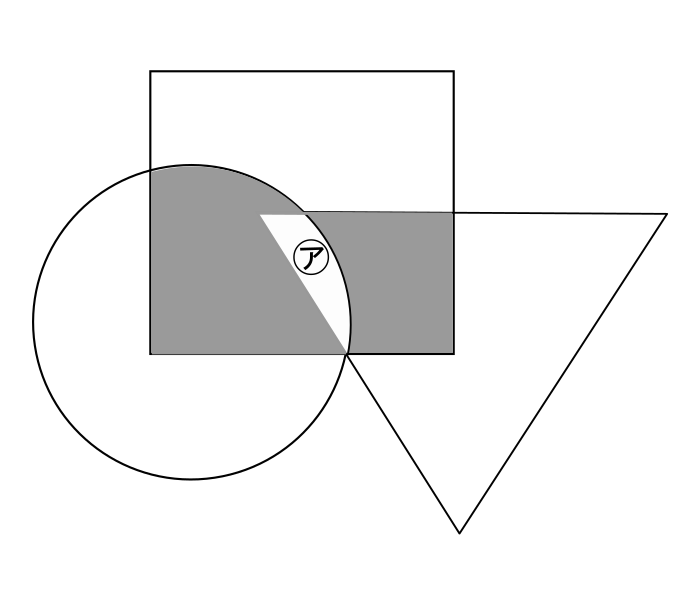
【問題】下の図のように, 円, 長方形, 三角形が重なっています。円, 長方形, 三角形のそれぞれの面積は $70\, \text{cm}^2$ , 図形全体の面積は $148\, \text{cm}^2$ , 3つの図形が重なっている㋐の部分の面積が $7\text{cm}^2$ のとき, 色のついた部分の面積を求めなさい。

【筑波大学附属中】

解答例

【解答例】
$70\text{cm}^2$ の面積が3つあるので全体としては, $70\times3=210\text{cm}^2$ なくてはならないが, 実際は $148\, \text{cm}^2$ しかない。この差し引いた面積は重なっている部分の面積になるので,
$210-148=62(\text{cm}^2)$
が重なりの部分の面積。
求めるのは色のついた部分なので, これから㋐の部分2つ分(2枚重なっているので)引いて面積を求める。
よって,
$62-7\times2=48\, \text{cm}^2$
$48\, \text{cm}^2\cdots$ (答)

2019筑波大学附属中

解答例

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル