こんにちは。立体の問題です。早速取り組んでいきましょう。
【問題】三角錐![]() があります。
があります。![]() ,
, ![]() とし,
とし, ![]() となる点Eを辺
となる点Eを辺![]() 上にとります。三角形OABの面積が
上にとります。三角形OABの面積が![]() のとき, 次の問いに答えなさい。
のとき, 次の問いに答えなさい。
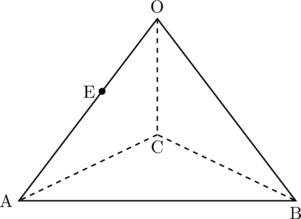
(1) 三角形OCEと三角形ACEの面積比を求めなさい。
(2) 底面を三角形EFGとするとき, 三角錐
(3) 四角錐
【麗澤中第一回AE】
【解答例】
(1) ![]() なので,
なので, ![]() (答)
(答)
(2)
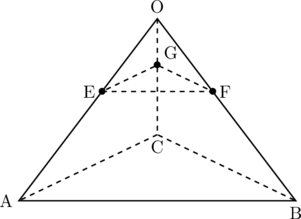
相似比は
よって求める側面積は,
(3)
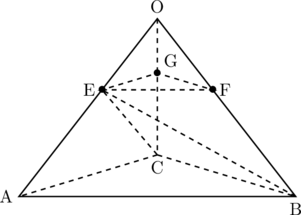
三角錐
三角錐
三角錐
よって, 四角錐
こんにちは。立体の問題です。早速取り組んでいきましょう。
【問題】三角錐![]() があります。
があります。![]() ,
, ![]() とし,
とし, ![]() となる点Eを辺
となる点Eを辺![]() 上にとります。三角形OABの面積が
上にとります。三角形OABの面積が![]() のとき, 次の問いに答えなさい。
のとき, 次の問いに答えなさい。

【解答例】
(1) ![]() なので,
なので, ![]() (答)
(答)
(2)

