こんにちは。空間ベクトルが, ![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸の正の向きとなす角を求める問題です。早速いってみましょう。
軸の正の向きとなす角を求める問題です。早速いってみましょう。
【問題】ベクトル![]() が,
が, ![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸の正の向きとなす角を, それぞれ,
軸の正の向きとなす角を, それぞれ, ![]() ,
, ![]() ,
, ![]() とするとき,
とするとき, ![]() の値をもとめ,
の値をもとめ, ![]() を求めよ。
を求めよ。
【解答・解説】![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸の正の方向の単位ベクトルをそれぞれ,
軸の正の方向の単位ベクトルをそれぞれ, ![]() とする。
とする。![]() と
と![]() の内積は,
の内積は, ![]()
![]() ,
, ![]() より,
より, 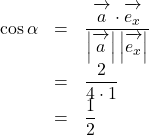
![]() より,
より, ![]()
![]() と
と![]() の内積は,
の内積は, ![]()
![]() ,
, ![]() より,
より, ![]()
![]() より,
より, ![]()
![]() と
と![]() の内積は,
の内積は, ![]()
![]() ,
, ![]() より,
より, 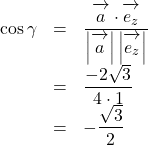
![]() より,
より, ![]()
以上より, ![]()
![]()
攻略ポイント
![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸の正の方向の単位ベクトルをそれぞれ,
軸の正の方向の単位ベクトルをそれぞれ, ![]() とする。
とする。
これを用いて, ![]() の値を求めていく。
の値を求めていく。
 数樂管理人のブログ
数樂管理人のブログ 


