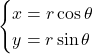こんにちは。今回は極座標についてです。
直交座標から説明すると, 直交座標とは言いかえると![]() 平面のことであり,
平面のことであり, ![]() 平面上にある点を
平面上にある点を![]() と表します。この点のことを直交座標と言います。それに対し, 極座標というものは, 直交座標で表された
と表します。この点のことを直交座標と言います。それに対し, 極座標というものは, 直交座標で表された![]() を原点Oからの距離
を原点Oからの距離![]() とその
とその![]() が
が![]() 軸の正の向きとなす角
軸の正の向きとなす角![]() で表した点
で表した点![]() のことを言います。
のことを言います。
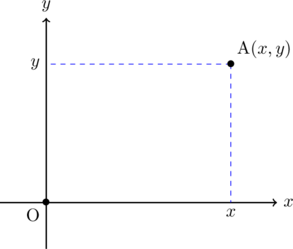
【直交座標A】
【極座標P】
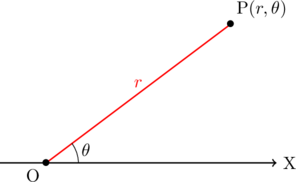
という。
極座標では,
上の2つの座標を重ねると,
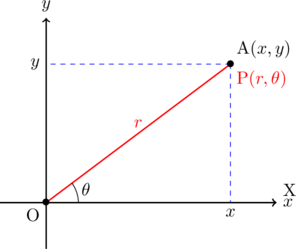
この図からわかるように,
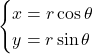
であり,
である。
また,
が得られる。
こんにちは。今回は極座標についてです。
直交座標から説明すると, 直交座標とは言いかえると![]() 平面のことであり,
平面のことであり, ![]() 平面上にある点を
平面上にある点を![]() と表します。この点のことを直交座標と言います。それに対し, 極座標というものは, 直交座標で表された
と表します。この点のことを直交座標と言います。それに対し, 極座標というものは, 直交座標で表された![]() を原点Oからの距離
を原点Oからの距離![]() とその
とその![]() が
が![]() 軸の正の向きとなす角
軸の正の向きとなす角![]() で表した点
で表した点![]() のことを言います。
のことを言います。
【直交座標A】


上の2つの座標を重ねると,