こんにちは。不定積分の難易度少し高めの問題です。早速いってみましょう。
【問題】![]() とおくことにより, 不定積分
とおくことにより, 不定積分![]() を求めよ。
を求めよ。
以下![]() とする。
とする。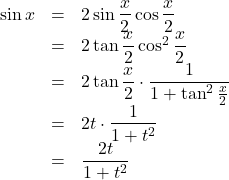
よって, ![]()
次に, 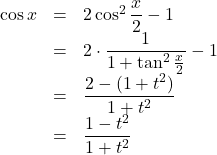
よって, ![]()
また, ![]() とし, 辺々を
とし, 辺々を![]() で微分すると,
で微分すると, 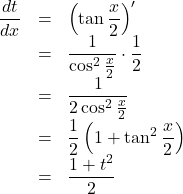
よって, ![]()
したがって, ![]()
![]() より,
より, 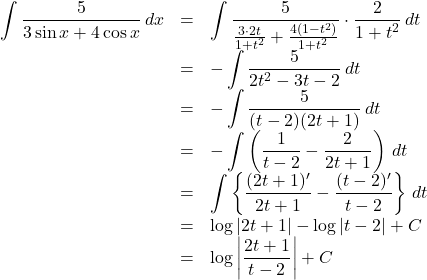
よって, 求める答えは, 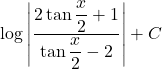 (
(![]() は積分定数)
は積分定数)
こんにちは。不定積分の難易度少し高めの問題です。早速いってみましょう。
【問題】![]() とおくことにより, 不定積分
とおくことにより, 不定積分![]() を求めよ。
を求めよ。
以下![]() とする。
とする。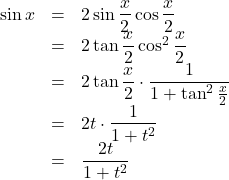
よって, ![]()
次に, 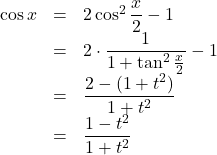
よって, ![]()
また, ![]() とし, 辺々を
とし, 辺々を![]() で微分すると,
で微分すると, 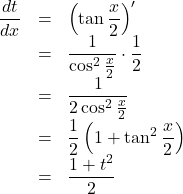
よって, ![]()
したがって, ![]()
![]() より,
より, 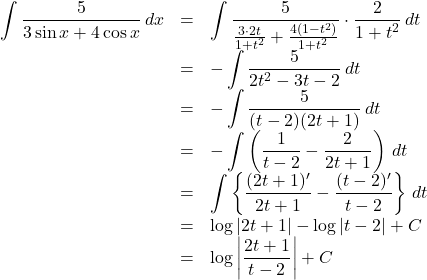
よって, 求める答えは, 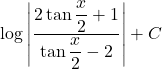 (
(![]() は積分定数)
は積分定数)