こんにちは。極座標で表す。直線や円の極方程式について書いておきます。
極Oを通り始線となす角が![]() の直線の極方程式は,
の直線の極方程式は, ![]()
で表される。
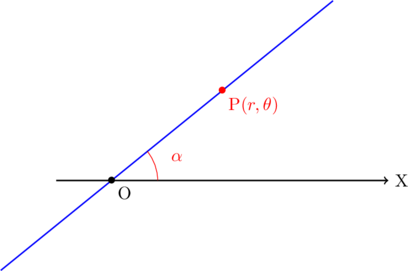
極座標では
点![]() を通り,
を通り, ![]() に垂直な直線の極方程式は,
に垂直な直線の極方程式は, ![]()
で表される。
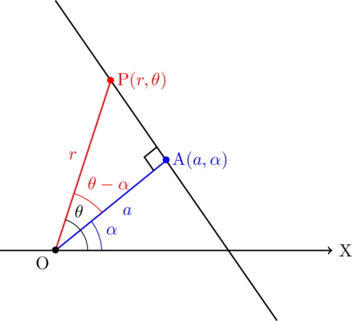
直角三角形OAPで
極Oが中心の円の極方程式は, ![]()
で表される。
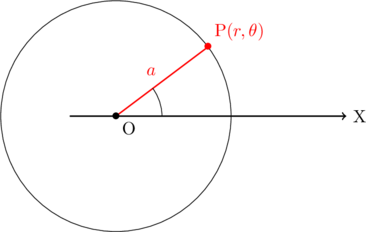
点![]() が中心で半径
が中心で半径![]() の円の極方程式は,
の円の極方程式は, ![]()
で表される。
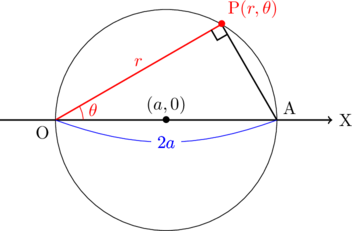
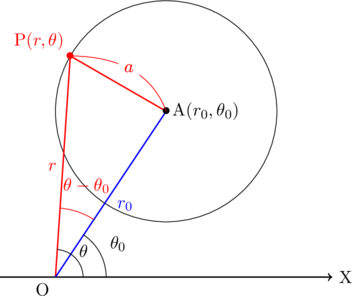
直角三角形OAPにおいて,
点![]() が中心で半径
が中心で半径![]() の円の極方程式は,
の円の極方程式は, ![]()
で表される。
この式は,
こんにちは。極座標で表す。直線や円の極方程式について書いておきます。
極Oを通り始線となす角が![]() の直線の極方程式は,
の直線の極方程式は, ![]()
で表される。

点![]() を通り,
を通り, ![]() に垂直な直線の極方程式は,
に垂直な直線の極方程式は, ![]()
で表される。

極Oが中心の円の極方程式は, ![]()
で表される。

点![]() が中心で半径
が中心で半径![]() の円の極方程式は,
の円の極方程式は, ![]()
で表される。

点![]() が中心で半径
が中心で半径![]() の円の極方程式は,
の円の極方程式は, ![]()
で表される。
