こんにちは。力ずくでも解けますが, それ以外の方法で解いてみましょう。
【問題】整式![]() を3次式とする。
を3次式とする。![]() が
が![]() で割り切れ,
で割り切れ, ![]() が
が![]() で割り切れるとき,
で割り切れるとき, ![]() を求めよ。
を求めよ。
【群馬大】
【解答・解説】
問題より, ![]()
![]()
![]() を
を![]() で割った余りと,
で割った余りと, ![]() を
を![]() で割った余りが等しいことに着目して問題を解いていく。
で割った余りが等しいことに着目して問題を解いていく。![]() より,
より, 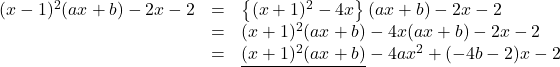
ここで, 下線部は![]() で割り切れるので,
で割り切れるので, ![]() を
を![]() で割った余りを求めると,
で割った余りを求めると, ![]() である。
である。
この余りが, ![]() 式を
式を![]() で割った余りと等しい。その余りは,
で割った余りと等しい。その余りは, ![]() であるから, 係数比較すると,
であるから, 係数比較すると, ![]()
![]()
これを解くと, ![]()
したがって, これを![]() に代入して,
に代入して, ![]()
よって, ![]() (答え)
(答え)
【別解】![]() ,
, ![]() の式を展開して, 係数比較しても求めることが可能である。
の式を展開して, 係数比較しても求めることが可能である。
このとき, ![]() ,
, ![]() となる。詳細は割愛する。
となる。詳細は割愛する。
 数樂管理人のブログ
数樂管理人のブログ 


