こんにちは。やっておきましょう。ケアレスミスに注意です。
【問題】数列![]() は
は![]() ,
, ![]()
をみたすものとする。
( i ) 数列![]() を
を![]() とするとき,
とするとき, ![]() の一般項を
の一般項を![]() と
と![]() を用いて表せ。
を用いて表せ。
( ii ) 数列![]() の一般項を
の一般項を![]() と
と![]() を用いて表せ。
を用いて表せ。
( iii ) すべての![]() について
について![]() をみたすような
をみたすような![]() の値を求めよ。
の値を求めよ。
【札幌医科大】
【解答解説】
( i ) 与式の両辺の対数をとると, 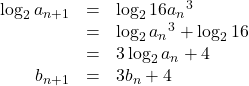
![]() が,
が, ![]() と変形できたとすると,
と変形できたとすると, ![]() なので,
なので, ![]() と変形できる。
と変形できる。
よって, 数列![]() は初項
は初項![]() , 公比3の等比数列である。
, 公比3の等比数列である。
したがって, ![]()
ゆえに, ![]() (答)
(答)
( ii )
( i )より, 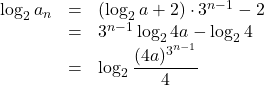
よって, ![]() (答)
(答)
( iii )
すべての![]() において
において![]() となるということは,
となるということは, ![]() の値によって,
の値によって, ![]() が変化しないことであるので,
が変化しないことであるので, ![]() の分子
の分子![]() の
の![]() が0か1であることが条件になる。
が0か1であることが条件になる。
ただし, ![]() なので,
なので, ![]() とはならない。
とはならない。
したがって, ![]() ,
, ![]() (答)
(答)
 高校数学:数列:log(対数)をとる漸化式の問題
高校数学:数列:log(対数)をとる漸化式の問題 数樂管理人のブログ
数樂管理人のブログ 


