高校数学：数列：log(対数)をとる漸化式の問題

こんにちは。今回は対数をとる漸化式の問題をやってみようと思います。例題を見ながらやっていきましょう。関連記事に演習問題載せてます。やってみてください。

例題を見てみよう

【例題】 $a_1=2$ , $a_{n+1}=8{a_n}^4$ によって定められる数列 $\{a_n\}$ の一般項 $a_n$ を求めよ。

両辺の対数をとって解いていく

【方針】 $a_{n+1}=p{a_n}^q$ の形で表される漸化式は両辺の対数をとってやることで解決します。
このときの対数の底は, $p$ や $a_1$ を素因数分解したときにできる数でやるとうまくいくことがあります。したがって, この場合, 底を2として両辺の対数をとることにします。ただ, 真数条件を満たすことを最初に示さないといけないので, それを書いてから解いていきます。
【解法】
$a_1=2>0$ で, 漸化式の形から数列 $\{a_n\}$ の一般項は正である。
両辺を底を2とする対数をとると,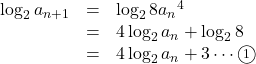
$\begin{array}{lll}\log_2{a_{n+1}}&=&\log_2{8{a_n}^4}\\&=&4\log_2{a_n}+\log_2{8}\\&=& 4\log_2{a_n}+3\cdots\maru1 \end{array}$
$\maru1$ が
$\log_2{a_{n+1}}+\alpha=4\left(\log_2{a_n}+\alpha\right)$
と表されるとすると, これは $\maru1$ と恒等な関係なので,
$\alpha=1$ となる。
したがって,
$\log_2{a_{n+1}}+1=4\left(\log_2{a_n}+1\right)$
となり, 数列 $\left\{\log_2{a_n}+1\right\}$ は, 初項 $\log_2{a_1}+1=1+1=2$ , 公比4の等比数列である。
よって,
$\log_2{a_n}+1=2\cdot4^{n-1}$
$\log_2{a_n}=2\cdot4^{n-1}-1$
となり,
$a_n=2^{2\cdot4^{n-1}-1}$
となる。

ここがポイント

$\maru1$ $a_{n+1}=p{a_n}^q$ の形で表される漸化式は両辺の対数をとってやることで解決します。このときの対数の底は, $p$ や $a_1$ を素因数分解したときにできる数でやるとうまくいくことがあります。ただ, 真数条件を満たすことを最初に示さないといけないので, それを書いてから解いていきます。
$\maru2$ 対数をとると, $\log_{b}{a_{n+1}}+q=p(\log_{b}{a_n}+q)$ の形の漸化式に落ち着くので, その漸化式を解いていくことになり, 最終的に対数の底 $b$ の累乗の形で表すことになります。