こんにちは。立体の最短距離とグラフにおける最短距離について考えていきます。
中学1年生の時に2点A,B間の最も短い線分のことを距離って言っていたと思います。このことを図形や座標軸に応用させたのが最短距離の問題です。典型的な問題を挙げてみてみましょう。
※立体にひもをかける問題
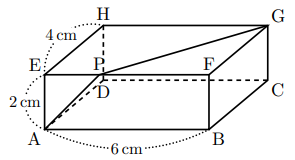
【問題】図1のように, ![]() ,
, ![]() ,
, ![]() の直方体があり, 頂点Aから頂点Gまで, 黒いひもを辺EFに交わるようにかける。黒いひもの長さが最も短くなるとき, 黒いひもと辺EFが交わる点をPとする。このとき, (1)~(3)の各問いに答えなさい。
の直方体があり, 頂点Aから頂点Gまで, 黒いひもを辺EFに交わるようにかける。黒いひもの長さが最も短くなるとき, 黒いひもと辺EFが交わる点をPとする。このとき, (1)~(3)の各問いに答えなさい。
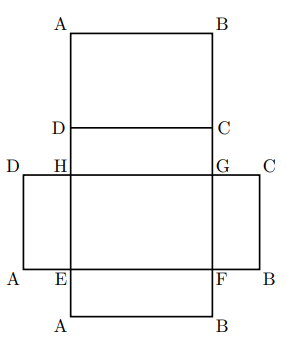
(1) 黒いひもが通る線を, 直方体の展開図(図2)に図示しなさい。
(2) 黒いひもの長さを求めなさい。
(3) 図1の直方体に, 頂点Bから頂点Dまで赤いひもを辺EF, 辺HGの順に交わるようにかける。
赤いひもの長さが最も短くなるとき, 赤いひもと辺EFが交わる点をQ, 赤いひもと辺HGが交わる点をR,
赤いひもと黒のひもが交わる点をSとする。このとき, (ア)~(エ)の各問いに答えなさい。
(ア) ![]() ∽
∽![]() であることを証明しなさい。
であることを証明しなさい。
(イ) HRの長さを求めなさい。
(ウ) RQの長さを求めなさい。
(エ) RSの長さを求めなさい。
【佐賀県】
この手の問題はまず間違いなく, 立体を展開図で考えるのがほとんど定石となっています。
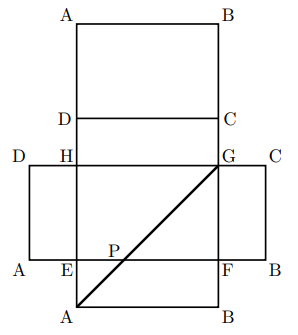
上の問題で, 線をかく問題が(1)にあるが, ひもが通っている面は2面である。また, AとGを結ぶ線は辺EFと交わることが図からわかる。だから, 答えは下のようになる。ひもがたるんでいては最短にならないので, 今回は点Aと点Gの2点間の距離そのものが最短になるので, それで答えを得ることができる。続きの(2)は三平方の定理, (3)は相似の問題として処理できる。典型的な問題なので, しっかり押さえておきましょう。
今回の問題では直方体を取り上げたが, よくある問題として円錐の最短距離問題がある。これも同様に側面の扇形の中心角を求めて, 展開図を書き線分を引いてその長さを求めるのが定石である。中心角によって解法は異なる。これに関しては典型パターンをまとめたのでこちらをクリックしてご覧ください。
※座標軸上での最短距離問題
【問題】座標軸上に2点A(![]() , 5), B(2, 1)がある。
, 5), B(2, 1)がある。![]() 軸上に点Pをとり,
軸上に点Pをとり, ![]() の長さが最も短くなるようにするとき, 点Pの座標を求めなさい。
の長さが最も短くなるようにするとき, 点Pの座標を求めなさい。
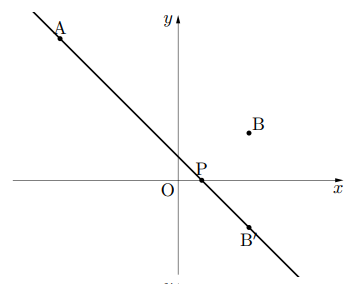
この手の問題は, 点Aまたは点Bを![]() 軸について対称に移動させて, その移動させた点と残りの点を結ぶ直線との交点が求める点Pになる。
軸について対称に移動させて, その移動させた点と残りの点を結ぶ直線との交点が求める点Pになる。
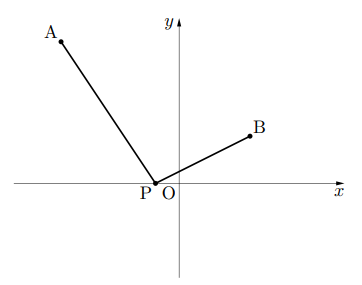
下図は点Bを![]() 軸に対称移動させB
軸に対称移動させB![]() とし, 点B
とし, 点B![]() と点Aを結んで点Pを求める図である。
と点Aを結んで点Pを求める図である。
今回はB![]() であることから, 直線AB
であることから, 直線AB![]() の式は
の式は![]() となる。従って球において求める点Pは(1, 0)である。
となる。従って球において求める点Pは(1, 0)である。
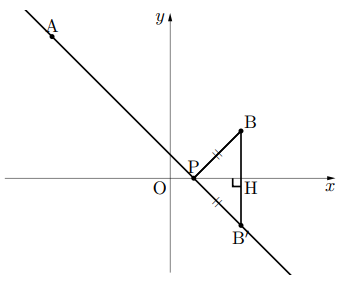
なぜこの方法で点Pが求まるかというと, 点Bが![]() 軸について対称な点をB
軸について対称な点をB![]() とすることで,
とすることで, ![]() となるため,
となるため, ![]() となり, 折れ線APBが線分AB
となり, 折れ線APBが線分AB![]() と等しくなることが分かる。こうやって, グラフ問題では最短距離問題を処理している。
と等しくなることが分かる。こうやって, グラフ問題では最短距離問題を処理している。
ここでも最短距離は直線で考えることができるという新しい発見があったようで, 数学をもっと好きになりますね。
 TikZ:中学数学:攻略法:円錐の最短距離問題典型パターンまとめ
TikZ:中学数学:攻略法:円錐の最短距離問題典型パターンまとめ 数樂管理人のブログ
数樂管理人のブログ