中学数学：立体と最短距離の問題(佐賀県)

こんにちは。早速いってみましょう。

佐賀県

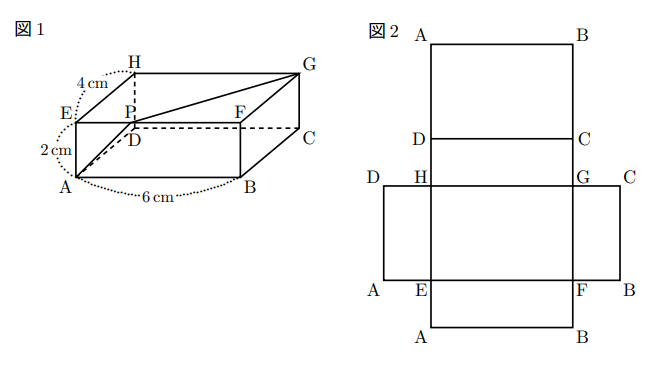
図1のように, cm, cm, cmの直方体があり, 頂点Aから頂点Gまで, 黒いひもを辺EFに交わるようにかける。黒いひもの長さが最も短くなるとき, 黒いひもと辺EFが交わる点をPとする。このとき, (1)～(3)の各問いに答えなさい。
(1) 黒いひもが通る線を, 直方体の展開図(図2)に図示しなさい。
(2) 黒いひもの長さを求めなさい。
(3) 図1の直方体に, 頂点Bから頂点Dまで赤いひもを辺EF, 辺HGの順に交わるようにかける。赤いひもの長さが最も短くなるとき, 赤いひもと辺EFが交わる点をQ, 赤いひもと辺HGが交わる点をR, 赤いひもと黒のひもが交わる点をSとする。このとき, (ア)～(エ)の各問いに答えなさい。
(ア) ∽であることを証明しなさい。
(イ) HRの長さを求めなさい。
(ウ) RQの長さを求めなさい。
(エ) RSの長さを求めなさい。
【佐賀県】

プリントアウト用pdf

解答pdf