中学数学：立体と最短距離の問題(福岡県)

こんにちは。それでは早速いってみましょう。

福岡県

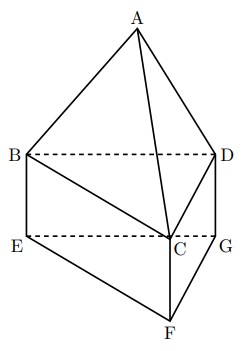
下の図は, 正四面体と三角柱を合わせた形で, 点A, B, C, D, E, F, Gを頂点とする立体を表している。正四面体ABCDの1辺の長さは4cmであり, 三角柱BCDEFGの側面はすべて合同な長方形である。
次の(1)～(3)に最も簡単な数で答えよ。ただし, 根号を使う場合はの中を最も小さい整数にすること。
(1) 図に示す立体において, 辺CDとねじれの位置にある辺は, 全部で何本あるか答えよ。
(2) 図に示す立体において, 辺BC上に点H, 辺AC上に点Iを, の長さが最も短くなるようにとる。cmのとき, の長さを求めよ。
(3) 図に示す立体において, 辺CD, DBの中点をそれぞれJ, Kとする。点Aと点Kを結び, 点Jを通り線分AKに垂直な直線と線分AKとの交点をLとする。三角すいLBJDの体積は, 正四面体ABCDの体積の何倍か求めよ。
【福岡県】

プリントアウト用pdf

解答pdf