中学数学：研究：発見？印を付けた角の和の公式

こんにちは。新しい？公式を考えてみました。それではどうぞ。

発見？印を付けた角の和の公式

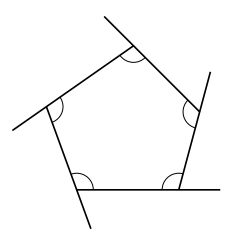
三角形や四角形をはじめ、多角形は1本の直線を折り曲げて作られています。この1つの多角形を1回転とします。
皆さん多角形の内角の和は $180\Deg\times(n-2)$ で与えられるのはご存知かと思います。このかっこの中の $-2$ とは $n$ 個ある頂点の1つの頂点から各頂点に引いたときにできる三角形の個数と中学校では習います。
ここでは少し観点を変えてみましょう。
上の公式 $180\Deg\times(n-2)$
のかっこをはずすと,
$180\Deg\times n-360\Deg$
となります。当たり前ですね。ここでポイントなのが $180\Deg$ は直線の角の大きさ, 360 $\Deg$ は外角の大きさです。上の図で直線(内角 $+$ 外角)はちょうど $n$ 個あり, その総和は $180\Deg\times n$ 。それから外角の総和360 $\Deg$ を引けば内角の和は求まります。そう考えてもおかしくはないでしょう。

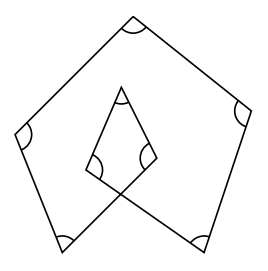
では次の図形を見てみましょう。
中学2年生でよく登場する, 印をつけた角というものを調査してみたいと思います。

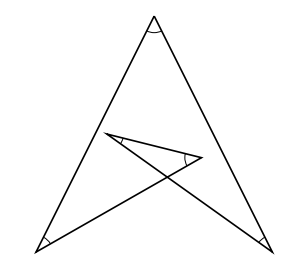
この図が, 先の五角形と違うのは1本の直線を2回転させているところです。この場合, 印をつけた角の和の大きさは $180\Deg$ です。
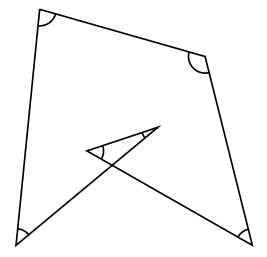
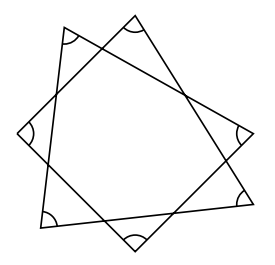
次に下図です。これも2回転のパターンです。印をつけた角の大きさは $360\Deg$ です。

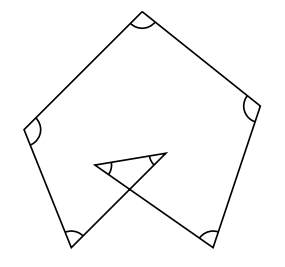
さらに下図です。これも2回転のパターンです。印をつけた角の大きさは $540\Deg$ です。その下にひとつ山を増やしました。山を増やすということは三角形の内角の和180 $\Deg$ 分角を大きくすることですから, 下の図の印をつけた角の和の大きさは720 $\Deg$ です。

中学生で出てくるほとんどは2回転です。
1回転は多角形の角の和の公式が使えます。
つまり, 1回転(多角形の内角の和) : $180\Deg\times(n-2)$
実は2回転にも公式?があるのを見つけました。まぁもともとあったのかもしれませんが?
それは,
2回転 : $180\Deg\times(m-4)$
$m$ は印をつけた山(mountain)の数です。
3回転は先に答えを言ってしまうと,
$180\Deg\times(m-6)$
$p$ 回転では,
$180\Deg\times(m-2p)$ となること間違いない?こういう発見をすると楽しいですよね。あってるかどうか分かりませんよ。実験して検証したらこうなったので, 一般化しただけです。下手の横好きなので, まぁそれもありかな。程度で考えてください。2回転は, 図中に多角形が2つできるような形になったり, 多角形を2枚重ねたような図形になります。それで大体区別できると思います。
では実際問題を解いてみましょう。
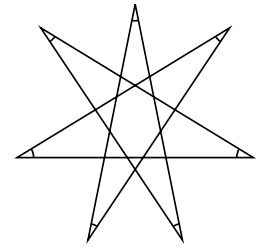
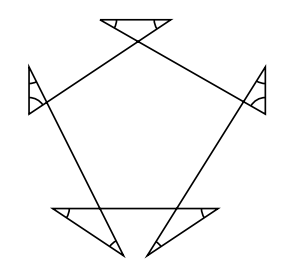
これは何回転?

山が7個あります。それで2回転です。ちょうど2枚の図形が重なったように見えます。
そして, 真中にその2つで囲まれた大きな七角形がありますよね。ですから2回転です。それで2回転 $180\Deg\times(m-4)$ を使うと,
$180\Deg\times(7-4)=540\Deg$
となります。
中学生ででてくるものは, ほとんどこのパターンで片付きます。例外もありますが, それは最後に書いてあります。

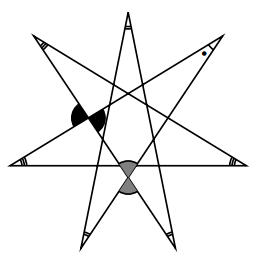
下の印をつけた角を求める前に、何回転でしょうか。

これは3回転です。ひと筆書きをしてみれば分かります。星形をかこうとして行き過ぎでまた戻ってきます。2回転ではなく3回転ですし, ちょうど3つの図形が重なったようになって真中に七角形ができていますよね。ですから, 公式 $180\Deg\times(m-6)$ を使うと, 山は7つなので,
$180\Deg\times(7-6)=180\Deg$ \となります。
実際正当な? 解き方をしても, 3つの二重線の角の和はグレーで塗った角になり, 3つの三重線の角の和は黒く塗った角になり, 結果として三角形の内角の和の大きさと同じになる。よって, 180 $\Deg$ になります。

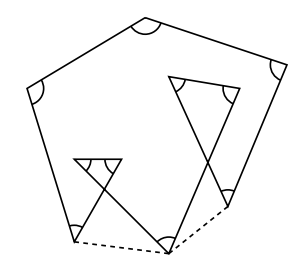
もう少し見てみましょう。下の2つの図で, 上の図は3回転の図, その下の図は4回転の図です。

印の数はそれぞれ, 上の図が10個, 下の図が13個です。上の図で, 印のついた角の和は, 公式 $180\Deg\times(m-2p)$ に $m=10, p=3$ を代入すると,
$180\Deg\times(10-6)=720\Deg$
実際に補助線(破線)を引いて考えると, 六角形の内角の和と同等なので,
$180\Deg\times(6-2)=720\Deg$
として与えられる。
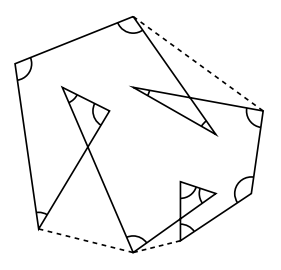
下の図も同様に, 公式 $180\Deg\times(m-2p)$ に $m=13, p=4$ を代入すると,
$180\Deg\times(13-8)=900\Deg$
実際に補助線(破線)を引いて考えると, 七角形の内角の和と同等なので,
$180\Deg\times(7-2)=900\Deg$
として与えられる。
ここまで述べてきたが, この公式が使えない場合がある。それは今までの印の付いた角は多角形がへこむことによって, 図形が発生するものだった。今回のものは多角形がへこむことなく印をつけた図形が外部にできる場合である。下の図のような場合, 印の付いた角の和は外角の和 $360\Deg$ と等しくなる。ただ, この場合も一般化すればできなくなさそうだが, 今回はここまでにしておこうと思う。