こんにちは。数学の世界の面白さを体感しよう。それではどうぞ。
数学では![]() ではなくて,
ではなくて, ![]() であることを証明しましょう。
であることを証明しましょう。
【証明】![]() とします。
とします。
この両辺10倍して, ![]() となります。
となります。
この![]() と
と![]() を筆算すると,
を筆算すると,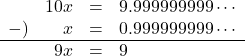
よって![]() 。もともと
。もともと![]() だったわけですので,
だったわけですので,![]()
ということがいえます。このように,
小数点以下9が無限に続く場合は, ほぼ1とみなされ, それはほぼ1ではなく1なのですね。
数学って面白いですね。
ちなみに, 循環小数を分数に直すときも同じような方法で行いますので, 上の解き方を知っておくと便利でしょう。
例 ![]() を分数で表しなさい。
を分数で表しなさい。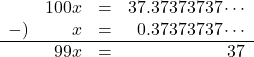
![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ 

