こんにちは。Short Time DFT(短時間フーリエ変換)についてです。
以下間違ってたらごめんなさいm(_)m。
Short time DFTは,瞬時スペクトラムの概念を導入することにより,
周波数分解能, 時間分解能をともに独立設定でき, 時間分解能を極限(サンプリング時刻)まで高めることができる。
時刻![]() の瞬時ペクトラム
の瞬時ペクトラム![]() は次のように与えられる。
は次のように与えられる。![]()
ここで![]() は瞬時スペクトラム
は瞬時スペクトラム![]() を構成するインデックス
を構成するインデックス![]() の成分であり, Short time DFTによって次のように定義される。
の成分であり, Short time DFTによって次のように定義される。![]()
但し, ![]() は入力信号,
は入力信号, ![]() はWindow関数,
はWindow関数, ![]() で与えられる回転演算子である。 次に, スペクトラム
で与えられる回転演算子である。 次に, スペクトラム![]() から
から![]() 個の出力信号を合成するShort time IDFTを次のように定義する。
個の出力信号を合成するShort time IDFTを次のように定義する。 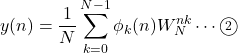
但し, ![]() はスペクトラム
はスペクトラム![]() から合成される時刻
から合成される時刻![]() の出力信号,
の出力信号, ![]() で与えられる回転演算子である。 ここで, スペクトラム
で与えられる回転演算子である。 ここで, スペクトラム![]() から合成される出力信号
から合成される出力信号![]() が, 瞬時スペクトラムのサンプリング時刻
が, 瞬時スペクトラムのサンプリング時刻![]() の入力信号
の入力信号![]() と一致することを証明する。
と一致することを証明する。![]() を
を![]() に代入すると
に代入すると 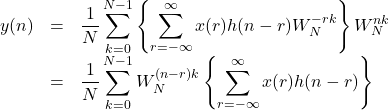
実際処理を行うときは上の![]() は有限長であるので,
は有限長であるので, ![]() の積和の順序は入れ替え可能である。
の積和の順序は入れ替え可能である。
ここで, 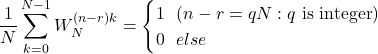
したがって, 出力![]() は
は![]() のときのみ値をもち, このとき
のときのみ値をもち, このとき![]() は次のように与えられる。
は次のように与えられる。 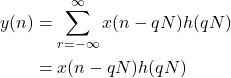
ここで, Window関数![]() に次の制約を設ける
に次の制約を設ける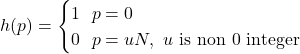
このとき, 出力信号![]() が, 時刻
が, 時刻![]() の入力信号
の入力信号![]() と一致することがわかる。このように, 時刻
と一致することがわかる。このように, 時刻![]() の瞬時スペクトラムからShort time IDFTを用いて合成される出力信号が, サンプリング時刻
の瞬時スペクトラムからShort time IDFTを用いて合成される出力信号が, サンプリング時刻![]() のみであることが知れる。これはDFTとは異なる点である。
のみであることが知れる。これはDFTとは異なる点である。
しかし, Short time DFTの完全系を満たすWindow関数は, 時刻![]() において1であり, Windowの中心
において1であり, Windowの中心![]() から時間
から時間![]() (
(![]() は0でない整数)において0を有すれば十分である(
は0でない整数)において0を有すれば十分である(![]() は未定義)。従って完全系を示すためのWindow関数は, 多数存在する。線型シフト不変のシステムの概念を加味すれば, Short time DFTは入力信号
は未定義)。従って完全系を示すためのWindow関数は, 多数存在する。線型シフト不変のシステムの概念を加味すれば, Short time DFTは入力信号![]() とインパルス
とインパルス![]() との畳み込み演算で与えられる。したがって, Short time DFTによって得られる瞬時スペクトラムは, インパルス応答
との畳み込み演算で与えられる。したがって, Short time DFTによって得られる瞬時スペクトラムは, インパルス応答![]() によって完全に記述される。つまり, Short time DFTはAM変調波とWindow関数の線型フィルタリングで与えられる。このことからもWindow関数の周波数応答の特性いかんでは,
によって完全に記述される。つまり, Short time DFTはAM変調波とWindow関数の線型フィルタリングで与えられる。このことからもWindow関数の周波数応答の特性いかんでは,
周波数解析, 周波数振幅解析, 位相解析に大きな影響を与えかねない。Short time DFTのWindow関数は大変重要であり, 上のWindow関数を満たす条件は完全系を示すだけのものでしかない。
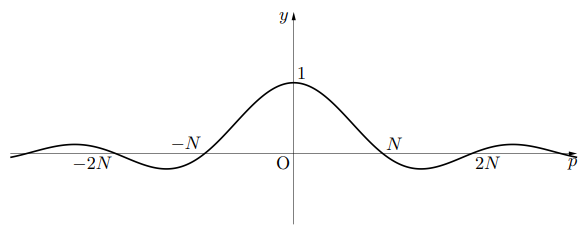
以下にShort time DFTのWindow関数の1つである, ナイキスト関数を書いてみた。![]()
 DFT(離散フーリエ変換)の完全系の証明
DFT(離散フーリエ変換)の完全系の証明
 DFT, Short Time DFTの行列表示
DFT, Short Time DFTの行列表示 数樂管理人のブログ
数樂管理人のブログ