こんにちは。DFT(離散フーリエ変換)についてです。それではどうぞ。
はじめに, ここにあるDFTなどの信号処理の文章は学生時代に勉強したものである。DFTはゼミで卒論の傍ら勉強していたものである。もちろん間違っていることがあることが予測されるので,
閲覧にはご注意を。emath, ![]() の練習です。ちなみに書いている本人は現在信号処理については記憶の彼方に消えている(笑)。ではご覧ください。
の練習です。ちなみに書いている本人は現在信号処理については記憶の彼方に消えている(笑)。ではご覧ください。
DFTとは入力信号に対してフレームの概念を導入することで, ![]() 個の入力信号から
個の入力信号から![]() 個の時間平均ともいえるスペクトラム成分を出力する。
個の時間平均ともいえるスペクトラム成分を出力する。
DFTから得られるスペクトラム![]() は次のように与えられる。
は次のように与えられる。![]()
ここで![]() はスペクトラム
はスペクトラム![]() を構成するインデックス
を構成するインデックス![]() の成分であり, DFTによって次のように定義される。
の成分であり, DFTによって次のように定義される。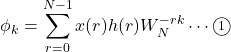
但し, ![]() は入力信号,
は入力信号, ![]() はWindow関数,
はWindow関数, ![]() で与えられる回転演算子である。
で与えられる回転演算子である。
次に, スペクトラム![]() から
から![]() 個の出力信号を合成するIDFTを次のように定義する。
個の出力信号を合成するIDFTを次のように定義する。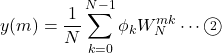
但し, ![]() はスペクトラム
はスペクトラム![]() から合成される出力信号,
から合成される出力信号, ![]() で与えられる回転演算子である。
で与えられる回転演算子である。
ここで, スペクトラム![]() から合成される出力信号
から合成される出力信号![]() が入力信号
が入力信号![]() と一致することを証明する。
と一致することを証明する。![]() を
を![]() に代入すると
に代入すると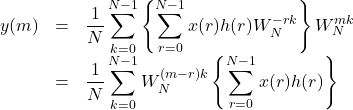
ここで, 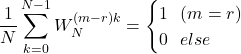
従って, 出力![]() は
は![]() のときのみ値をもち, このとき
のときのみ値をもち, このとき![]() は次のように与えられる。
は次のように与えられる。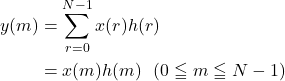
ここで, Window関数![]() は重み1の関数であるから,
は重み1の関数であるから,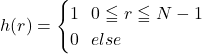
このとき, ![]() 個の出力信号が,
個の出力信号が, ![]() 個の入力信号と一致することがわかる。
個の入力信号と一致することがわかる。
 Short Time DFT(短時間フーリエ変換)の完全系の証明
Short Time DFT(短時間フーリエ変換)の完全系の証明
 DFT, Short Time DFTの行列表示
DFT, Short Time DFTの行列表示 数樂管理人のブログ
数樂管理人のブログ 
