こんにちは。定期テスト対策です。それではどうぞ。
ある高校における男子の身長![]() が, 平均170.9cm, 標準偏差5.4cmの正規分布に従うものとするとき, 身長175cm以上の生徒は約何
が, 平均170.9cm, 標準偏差5.4cmの正規分布に従うものとするとき, 身長175cm以上の生徒は約何![]() いるか。ただし,
いるか。ただし, ![]() は小数第3位を四捨五入して小数第2位まで,
は小数第3位を四捨五入して小数第2位まで, ![]() は小数第2位を四捨五入して小数第1位まで求めよ。
は小数第2位を四捨五入して小数第1位まで求めよ。![]() は正規分布
は正規分布![]() に従うから,
に従うから, 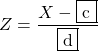 とおくと,
とおくと, ![]() は標準正規分布
は標準正規分布![]() に従う。
に従う。![]()
よって, 175cm以上の生徒は約![]() いる。
いる。
【解答】![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
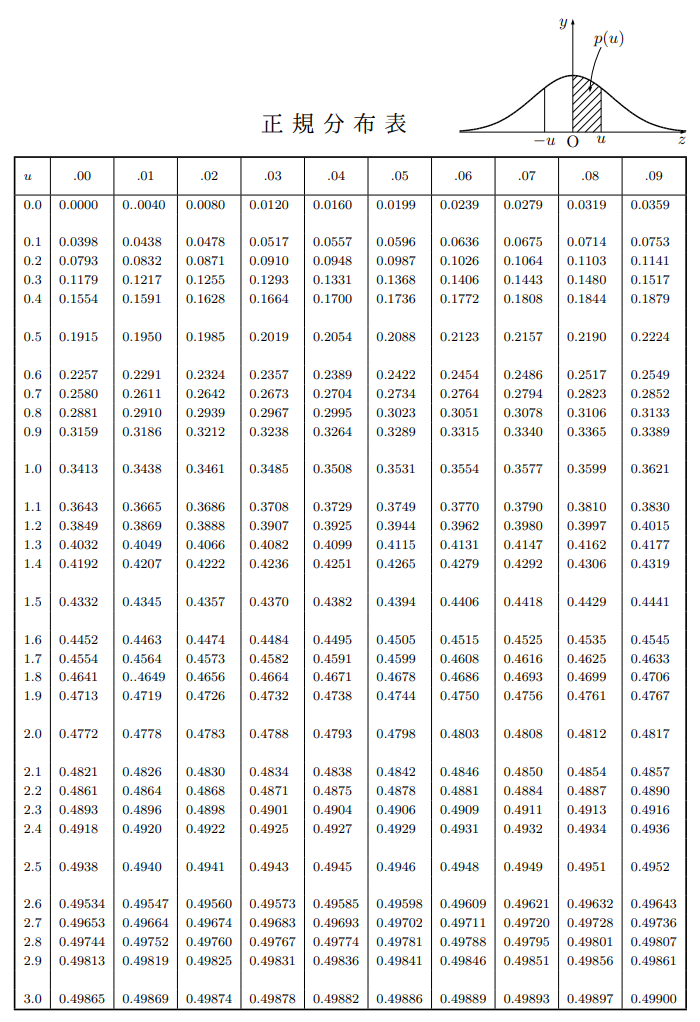
【解説】![]() より,
より, ![]() となるのは,
となるのは, ![]()
よって, ![]()
正規分布より![]() の値が0.2764なので,
の値が0.2764なので, ![]() の値は
の値は![]()
 数樂管理人のブログ
数樂管理人のブログ