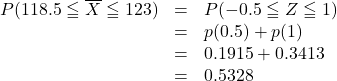こんにちは。定期テスト対策です。
母平均120, 母標準偏差30をもつ母集団から, 大きさ100の無作為標本を抽出するとき, 次の![]() ~
~![]() に当てはまる数を求めよ。
に当てはまる数を求めよ。
その標本平均![]() の平均
の平均![]() , 標準偏差
, 標準偏差![]()
よって, ![]() が118.5以上123以下の値をとる確率は
が118.5以上123以下の値をとる確率は![]() である。
である。
【解答】
➀ 120
➁ 3
➂ 0.5328
【解説】![]() は近似的に正規分布,
は近似的に正規分布, ![]() , すなわち,
, すなわち, ![]() にしたがう。
にしたがう。
よって, ![]() は近似的に標準正規分布
は近似的に標準正規分布![]() にしたがう。
にしたがう。
したがって, 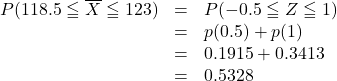
こんにちは。定期テスト対策です。
母平均120, 母標準偏差30をもつ母集団から, 大きさ100の無作為標本を抽出するとき, 次の![]() ~
~![]() に当てはまる数を求めよ。
に当てはまる数を求めよ。
その標本平均![]() の平均
の平均![]() , 標準偏差
, 標準偏差![]()
よって, ![]() が118.5以上123以下の値をとる確率は
が118.5以上123以下の値をとる確率は![]() である。
である。
【解答】
➀ 120
➁ 3
➂ 0.5328
【解説】![]() は近似的に正規分布,
は近似的に正規分布, ![]() , すなわち,
, すなわち, ![]() にしたがう。
にしたがう。
よって, ![]() は近似的に標準正規分布
は近似的に標準正規分布![]() にしたがう。
にしたがう。
したがって,