TikZ：受験算数：面積(明治大学付属中野中学)

こんにちは。早速いってみましょう。

明治大学付属中野中学

下の図のように，半径9cmの円の周上を4等分した点を結んで正方形をかき，さらに，この正方形のそれぞれの辺を3等分した点をとり，小さい正方形ができるように点を結びました。このとき，斜線部分の面積の和を求めなさい。ただし，円周率は3.14とします。

解答・解説

【解答】 $182.34\text{cm}^2$
【解説】
3等分点をそれぞれまっすぐ結んで小さな正方形に分割すると見やすくなる。

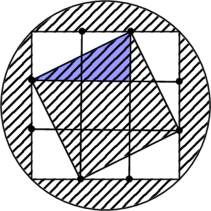
図中の一番大きい正方形は対角線が直径18cmのものなので，その面積は
$18\times18\times\dfrac12=162$
円の面積は
$9\times9\times3.14=254.34$
したがって，外側の斜線部分の面積は
$254.34-162=92.34\cdots\maru1$
二番目に大きい正方形の面積は，
色でぬった三角形が4つの面積と真ん中の一番小さい正方形の面積の和で求められるので，
色でぬった三角形の面積は一番大きい正方形の面積の $\dfrac29$ の半分であるから，
$162\times\dfrac19=18$
一番小さい正方形も一番大きい正方形の $\dfrac19$ であるから，面積は $18$
よって二番目に大きい正方形の面積は $18\times5=90\cdots\maru2$
したがって，求める面積は $\maru1$ ， $\maru2$ より，
$92.34+90=182.34$

明治大学付属中野中学

解答・解説

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル