こんにちは。今回は分数型の数列の解法を書いておきます。例題を見ながらいきましょう。
シンプルな分数型は逆数で考える
【例】![]() ,
, ![]() で定義される数列の一般項
で定義される数列の一般項![]() を求めよ。
を求めよ。
【解法】![]() とすると, 与式より
とすると, 与式より![]() ,
, ![]() なら
なら![]() となり, これを繰り返すと,
となり, これを繰り返すと, ![]() となるが,
となるが, ![]() であるので矛盾する。よって,
であるので矛盾する。よって, ![]()
このとき, 与式の両辺の逆数をとると, 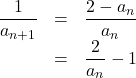
ここで, ![]() とおくと,
とおくと, ![]()
式変形すると![]()
数列![]() は初項
は初項![]() , 公比2の等比数列である。
, 公比2の等比数列である。
よって, ![]()
![]()
となり, ![]()
から![]()
となる。
※![]() の変形に特性方程式を用いるが答案には書かない方がよい。
の変形に特性方程式を用いるが答案には書かない方がよい。
特性方程式:![]() の漸化式
の漸化式![]() を
を![]() として得られる
として得られる![]() を用いる手法。
を用いる手法。
分数型の漸化式①
 数樂管理人のブログ
数樂管理人のブログ 

