こんにちは。今回は分数型の漸化式を見ていきましょう分数型の漸化式①より複雑なものになります。例題を見ながらいきましょう。
特性方程式から誘導に乗ろう
【例】数列![]() が漸化式
が漸化式![]()
で与えられている。このとき, 次の問いに答えよ。
(1) ![]() の2つの解を
の2つの解を![]() とする。
とする。![]() とするとき, 数列
とするとき, 数列![]() は等比数列になることを示せ。
は等比数列になることを示せ。
(2) 数列![]() の一般項を求めよ。
の一般項を求めよ。
【解法】![]() から,
から, ![]()
![]()
![]()
![]() より,
より, ![]()
したがって,![]() となり,
となり, ![]() となる。
となる。![]()
ここで, ![]() の分子と分母をそれぞれ計算すると,
の分子と分母をそれぞれ計算すると,
分子は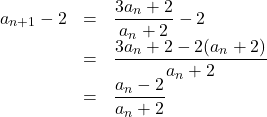
分母は
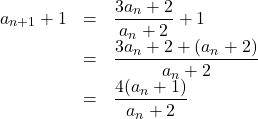
したがって, ![]() は,
は,![]()
よって, ![]() となり, 数列
となり, 数列![]() は等比数列になることが示せた。
は等比数列になることが示せた。
(2) ![]()
となり, ![]() は初項
は初項![]() 公比
公比![]() の等比数列である。
の等比数列である。![]()
![]()
![]()
![]()
![]()
![]() (答)
(答)
今回は問題文に![]() の二次方程式となる特性方程式が登場しましたが, 普通は載っていないので, 自分で
の二次方程式となる特性方程式が登場しましたが, 普通は載っていないので, 自分で![]() を
を![]() とおいて, 特性方程式をつくって解いてください。あとは問題に沿うように解いていけば問題ないと思います。ただし, 特性方程式は答案用紙には書かない方がよいです。
とおいて, 特性方程式をつくって解いてください。あとは問題に沿うように解いていけば問題ないと思います。ただし, 特性方程式は答案用紙には書かない方がよいです。
分数型の漸化式②
特性方程式を解いて, 問題文にしたがって, 等比数列の形に持ち込もう。
 数樂管理人のブログ
数樂管理人のブログ 

