こんにちは。今回は自然対数![]() のお話です。
のお話です。
![]() を導関数の定義にしたがって, 微分すると,
を導関数の定義にしたがって, 微分すると, 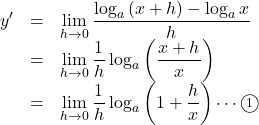
ここで, ![]() とおくと,
とおくと, ![]() であるから,
であるから, ![]() , また,
, また, ![]() なので,
なので, ![]() を書き換えると,
を書き換えると, 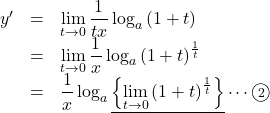
![]() の下線部を実際に計算すると, (CASIO電卓による計算)
の下線部を実際に計算すると, (CASIO電卓による計算)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
となり, この極限値を自然対数![]() と定義します。
と定義します。![]() は
は![]() という無理数になります。
という無理数になります。
自然対数![]() は次のように定義する。
は次のように定義する。![]()
または, ![]()
![]() で
で![]() とおくと,
とおくと, ![]() のとき,
のとき, ![]() で,
で, ![]() になるので,
になるので, ![]() 式が得られる。
式が得られる。
【問題】次の極限値を求めよ。![]()
![]()
![]()
![]()
![]()
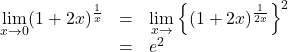
![]()
![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\lim_{x\to\infty}\left(1+\dfrac1x\right)^{\frac x3}&=&\displaystyle\lim_{x\to\infty}\left\{\left(1+\dfrac1x\right)^x\right\}^{\frac13}\\&=&\sqrt[3]{e}\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-5c162a2f58de26630b599e0e73f54549_l3.png)
![]()
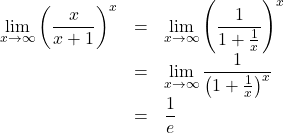
![]()
![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\lim_{x\to\infty}\left(1-\dfrac{1}{x}\right)^{2x}&=&\displaystyle\lim_{x\to\infty}\left[\left\{1+\left(-\dfrac{1}{x}\right)\right\}^{-x}\right]^{-2}\\&=&e^{-2}\\&=&\dfrac{1}{e^2}\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-f0f30acb27aada80cd1311196bca3fee_l3.png)
こんにちは。今回は自然対数![]() のお話です。
のお話です。
![]() を導関数の定義にしたがって, 微分すると,
を導関数の定義にしたがって, 微分すると, 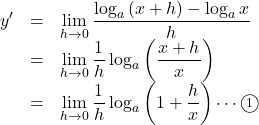
ここで, ![]() とおくと,
とおくと, ![]() であるから,
であるから, ![]() , また,
, また, ![]() なので,
なので, ![]() を書き換えると,
を書き換えると, 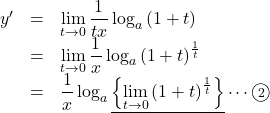
![]() の下線部を実際に計算すると, (CASIO電卓による計算)
の下線部を実際に計算すると, (CASIO電卓による計算)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
となり, この極限値を自然対数![]() と定義します。
と定義します。![]() は
は![]() という無理数になります。
という無理数になります。
自然対数![]() は次のように定義する。
は次のように定義する。![]()
または, ![]()
![]() で
で![]() とおくと,
とおくと, ![]() のとき,
のとき, ![]() で,
で, ![]() になるので,
になるので, ![]() 式が得られる。
式が得られる。
【問題】次の極限値を求めよ。![]()
![]()
![]()
![]()
![]()
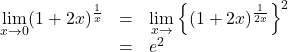
![]()
![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\lim_{x\to\infty}\left(1+\dfrac1x\right)^{\frac x3}&=&\displaystyle\lim_{x\to\infty}\left\{\left(1+\dfrac1x\right)^x\right\}^{\frac13}\\&=&\sqrt[3]{e}\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-5c162a2f58de26630b599e0e73f54549_l3.png)
![]()
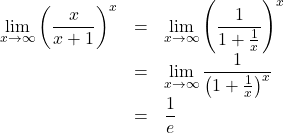
![]()
![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\lim_{x\to\infty}\left(1-\dfrac{1}{x}\right)^{2x}&=&\displaystyle\lim_{x\to\infty}\left[\left\{1+\left(-\dfrac{1}{x}\right)\right\}^{-x}\right]^{-2}\\&=&e^{-2}\\&=&\dfrac{1}{e^2}\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-f0f30acb27aada80cd1311196bca3fee_l3.png)