こんにちは。三角関数を含む方程式の解の個数についての解法を記しておきます。例題をやりながら見ていきましょう。
【例題】![]() のとき, 方程式
のとき, 方程式![]() の解の個数を, 定数
の解の個数を, 定数![]() の値によって分類しなさい。
の値によって分類しなさい。
【方針】定数分離の考え方を用いる。
定数分離とは等式を定数と定数でない部分に分けることを言い, 今回の場合なら, 等式を![]()
と定数部分を右辺に移項する。そして, ![]() と
と![]() の交点の個数から, 方程式の解の個数を調べる方法のことである。
の交点の個数から, 方程式の解の個数を調べる方法のことである。
【解答例】
等式を![]() とし,
とし, ![]() と
と![]() とする。
とする。![]() は
は![]() より,
より, ![]()
となる。ここで, 考えやすいように, ![]() とおくと,
とおくと, ![]() となり,
となり, ![]() より,
より, ![]() となる。
となる。
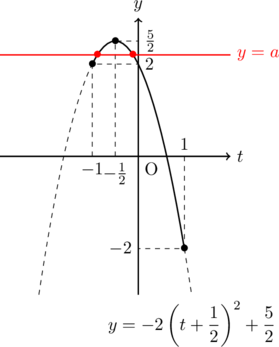
平方完成すると, ![]()
![]() の範囲でグラフをかくと,
の範囲でグラフをかくと,
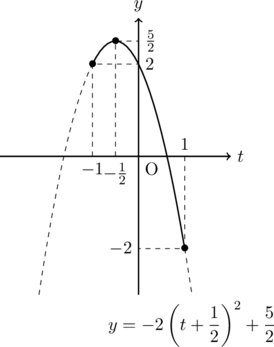
となる。
これと
(A)
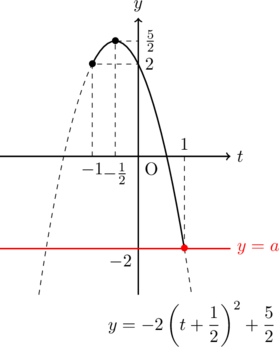
(B)
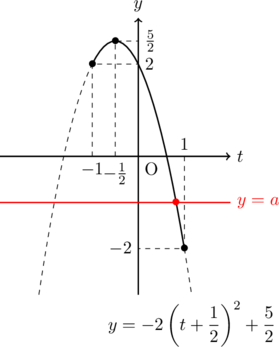
(C)
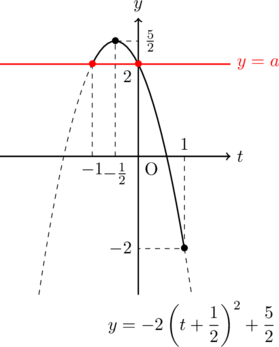
(D)
(E)

以上(A)~(E)をまとめると,
となる。
押さえておくべきポイント
![]() 今回のような定数分離の解法は頻出なので, しっかりと押さえておくこと。
今回のような定数分離の解法は頻出なので, しっかりと押さえておくこと。![]()
![]() や
や![]() の解が1や
の解が1や![]() になる
になる![]() の値は基本1つしかなく, それ以外は1つの値に対して, それを満たす
の値は基本1つしかなく, それ以外は1つの値に対して, それを満たす![]() の値は基本2つあることもことも押さえておきましょう。
の値は基本2つあることもことも押さえておきましょう。
 数樂管理人のブログ
数樂管理人のブログ 

