TikZ：中学数学：空間図形：立体の体積(岩手県)

こんにちは。立体の体積に関しては受験算数の問題(中1生でもできます)ですね。中2以下は(2)のみやってみてください。それではいってみましょう。

岩手県

下の図は, $\mathrm{AB}=6\,\text{cm}$ , $\mathrm{AD}=5\,\text{cm}$ , $\mathrm{AE}=7\,\text{cm}$ の直方体 $\mathrm{ABCD-EFGH}$ です。このとき, 次の(1), (2)の問いに答えなさい。
(1) 線分 $\mathrm{AF}$ の長さを求めなさい。
(2) 辺CG上に, $\mathrm{PG}=2\,\text{cm}$ となるような点Pをとったとき, 四面体AHFPの体積を求めなさい。

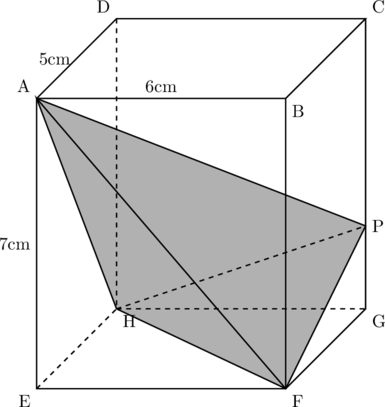
【2023岩手県】

解答例

【解答例】
(1) 三平方の定理より,
$\text{AF}=\sqrt{7^2+6^2}=\sqrt{85}$
$\sqrt{85}\,\text{cm}\cdots$ (答)
(2) 【方針】
(四面体 $\mathrm{AHFP}$ ) $=$ (直方体 $\mathrm{ABCD-EFGH}$ )－(三角錐 $\mathrm{P-GFH}$ )－(三角錐 $\mathrm{A-EFH}$ )－(四角錐 $\mathrm{A-CPFB}$ )－(四角錐 $\mathrm{A-CPHD}$ )
として求める。
解答例
$\maru1$ 直方体 $\mathrm{ABCD-EFGH}$ の体積
$5\times6\times7=210$
$\maru2$ 三角錐 $\mathrm{P-GFH}$ の体積
$5\times6\times\dfrac12\times2\times\dfrac13=10$
$\maru3$ 三角錐 $\mathrm{A-EFH}$ の体積
$5\times6\times\dfrac12\times7\times\dfrac13=35$
$\maru4$ 四角錐 $\mathrm{A-CPFB}$ の体積
$(5+7)\times5\times\dfrac12\times6\times\dfrac13=60$
$\maru5$ 四角錐 $\mathrm{A-CPHD}$ の体積
$(5+7)\times6\times\dfrac12\times5\times\dfrac13=60$
$\maru1$ ～ $\maru5$ より, 求める体積は,
$210-10-35-60-60=210-165=45$
$45\,\mathrm{cm^3}\cdots$ (答)

岩手県

解答例

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル