こんにちは。円錐の最短距離の典型問題でおうぎ形の中心角によって求め方が違うのでその例を示しておきます。
円錐の底面の点Aから側面を通ってひもをかけて再び点Aに戻るとき, ひもの長さが最も短くなる長さを一般的に最短距離と言います。下図の赤線部
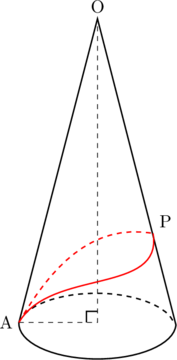
側面をつくるおうぎ形の中心角が求まらなければ, 最短距離も求められません。求め方の公式を確認しておきましょう。円錐の母線![]() , 底面の半径
, 底面の半径![]() , 側面を展開図にしたときのおうぎ形の中心角を
, 側面を展開図にしたときのおうぎ形の中心角を![]() とする。
とする。
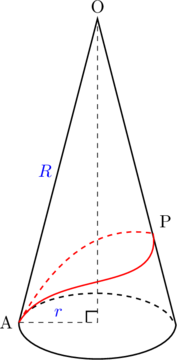
証明はこちらをご覧ください。

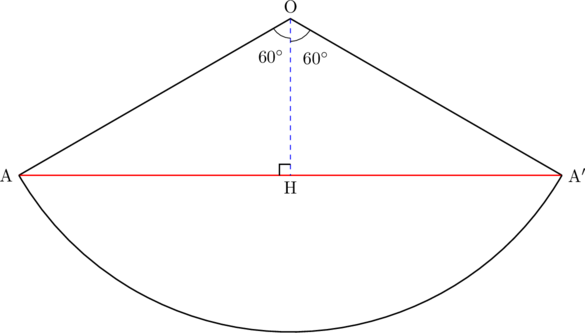
【![]() の場合】
の場合】![]() は正三角形になる。最短距離(赤線分)の長さは正三角形の1辺(母線の長さ)と一致する。
は正三角形になる。最短距離(赤線分)の長さは正三角形の1辺(母線の長さ)と一致する。

【

【演習問題】
 中学数学:空間図形:円錐と最短距離の問題(典型問題①)
中学数学:空間図形:円錐と最短距離の問題(典型問題①)【![]() の場合】
の場合】![]() は頂角
は頂角![]() の二等辺三角形になる。頂点Oから線分
の二等辺三角形になる。頂点Oから線分![]() に垂線を
に垂線を![]() 下ろし,
下ろし, ![]() の直角三角形
の直角三角形![]() をつくって最短距離(赤線分)の長さを求める。
をつくって最短距離(赤線分)の長さを求める。
【演習問題】
 中学数学:空間図形:円錐と最短距離の問題(典型問題②)
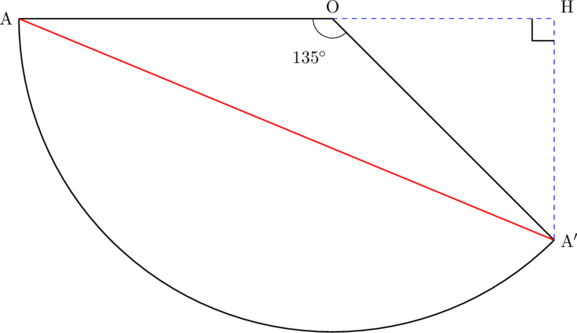
中学数学:空間図形:円錐と最短距離の問題(典型問題②)【![]() の場合】
の場合】![]() は頂角
は頂角![]() の二等辺三角形になる。この場合は, おうぎ形の外側に直角二等辺三角形
の二等辺三角形になる。この場合は, おうぎ形の外側に直角二等辺三角形![]() をつくり,
をつくり, ![]() の長さから,
の長さから, ![]() ,
, ![]() の長さを求め, 最終的に直角三角形
の長さを求め, 最終的に直角三角形![]() で三平方の定理より最短距離(赤線分)の長さを求める。ただ, この方法でいくと, 赤線部は二重根号(高校生の範囲)となるので, 中心角が
で三平方の定理より最短距離(赤線分)の長さを求める。ただ, この方法でいくと, 赤線部は二重根号(高校生の範囲)となるので, 中心角が![]() になる場合,
になる場合, ![]() を求めさせるか,
を求めさせるか, ![]() と何かで囲まれた図形の面積を求める問題に置き換わることが考えられる。
と何かで囲まれた図形の面積を求める問題に置き換わることが考えられる。
【演習問題】
 中学数学:空間図形:円錐と最短距離の問題(典型問題③)
中学数学:空間図形:円錐と最短距離の問題(典型問題③) 中学数学:攻略法:最短距離に関する問題のコツ
中学数学:攻略法:最短距離に関する問題のコツ 数樂管理人のブログ
数樂管理人のブログ 

