TikZ：高校数学：数III積分：アステロイド曲線とその長さ

こんにちは。早速いってみましょう。

問題

【問題】 $a>0$ , $0\leqq\theta\leqq2\pi$ とし, 媒介変数表示
$\begin{cases}x=a\cos^3\theta\\y=a\sin^3\theta\end{cases}$
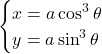
で表される曲線のグラフをかき, その長さを求めよ。

解答・解説

【解答例】
$x=a\cos^3\theta$ を $\theta$ で微分すると,
$\dfrac{dx}{d\theta}=-3a\sin\theta\cos^2\theta$
$\cos^2\theta\geqq0$ より, 符号は $\sin\theta$ の符号の逆になる(マイナスが付いているため)。
$y=a\sin^3\theta$ を $\theta$ で微分すると,
$\dfrac{dy}{d\theta}=3a\sin^2\cos\theta$
$\sin^2\theta\geqq0$ より, 符号は $\cos\theta$ の符号で決まる。
これより,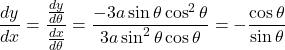
$\dfrac{dy}{dx}=\dfrac{\frac{dy}{d\theta}}{\frac{dx}{d\theta}}=\dfrac{-3a\sin\theta\cos^2\theta}{3a\sin^2\theta\cos\theta}=-\dfrac{\cos\theta}{\sin\theta}$
となる。以上のことから,
$0\leqq\theta\leqq\dfrac{\pi}{2}\cdots\maru1$
$\dfrac{\pi}{2}\leqq\theta\leqq\pi\cdots\maru2$
$\pi\leqq\theta\leqq\dfrac{3}{2}\pi\cdots\maru3$
$\dfrac32\pi\leqq\theta\leqq2\pi\cdots\maru4$
に分けて考えなくてはならない。
$\maru1$ のとき, $\cos\theta>0, \sin\theta>0$ より, $\dfrac{dx}{d\theta}<0, \dfrac{dy}{d\theta}>0$
$\to\theta$ が増加すると, $x$ は減少し, $y$ は増加する。
$\maru2$ のとき, $\cos\theta<0, \sin\theta>0$ より, $\dfrac{dx}{d\theta}<0, \dfrac{dy}{d\theta}<0$
$\to\theta$ が増加すると, $x$ は減少し, $y$ は減少する。
$\maru3$ のとき, $\cos\theta<0, \sin\theta<0$ より, $\dfrac{dx}{d\theta}>0, \dfrac{dy}{d\theta}<0$
$\to\theta$ が増加すると, $x$ は増加し, $y$ は減少する。
$\maru4$ のとき, $\cos\theta>0, \sin\theta<0$ より, $\dfrac{dx}{d\theta}>0, \dfrac{dy}{d\theta}>0$
$\to\theta$ が増加すると, $x$ は増加し, $y$ は増加する。
また,
$a\cos^3(\pi-\theta)=-a\cos^3\theta=-x$
$a\sin^3(\pi-\theta)=a\sin^3\theta=y$
となるので, グラフは $y$ 軸対称である。
$a\cos^3(2\pi-\theta)=a\cos^3\theta=x$
$a\sin^3(2\pi-\theta)=-a\sin^3\theta=-y$
となるので, グラフは $x$ 軸対称でもある。
$\theta=0, \dfrac{\pi}{2}, \pi, \dfrac{3}{2}\pi, 2\pi$ の他に, $\theta=\dfrac{\pi}{4},\dfrac34\pi,\dfrac54\pi,\dfrac74\pi$ の点などを参考にして, グラフを描くと以下のようになる。

次に曲線の長さを求める。
求める弧の長さ $L$ は $0\leqq\theta\leqq\dfrac{\pi}{2}$ の範囲 $(0\leqq\sin\theta\leqq1, 0\leqq\cos\theta\leqq1)$ の長さを求めて4倍すればよい。
$\dfrac{dx}{d\theta}=-3a\sin\theta\cos^2\theta$ , $\dfrac{dy}{d\theta}=3a\sin^2\cos\theta$ である。
したがって, 次のようになる。
$\begin{array}{lll}L&=&4\displaystyle\int_0^{\frac{\pi}{2}}\sqrt{\left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta}\right)^2}\,d\theta\\&=&4\displaystyle\int_0^{\frac{\pi}{2}}\sqrt{(-3a\sin\theta\cos^2\theta)^2+(3a\sin^2\cos\theta)^2}\,d\theta\\&=&4\displaystyle\int_0^{\frac{\pi}{2}}\sqrt{9a^2\cos^2\sin^2\theta(\cos^2\theta+\sin^2\theta)}\,d\theta\\&=&4\displaystyle\int_0^{\frac{\pi}{2}}3a\sin\theta\cos\theta\,d\theta\\&=&6a\displaystyle\int_0^{\frac{\pi}{2}}\sin2\theta\,d\theta\\&=&6a\left[-\dfrac12\cos2\theta\right]_0^{\frac{\pi}{2}}\\&=&6a\left\{\dfrac12-\left(-\dfrac12\right)\right\}\\&=&6a\end{array}$
よって, 弧の長さは $6a$
この曲線はアステロイド曲線と言います。以下の関連記事に性質をまとめています。ご覧ください。

2023年5月3日TikZ：高校数学：数IIIグラフ：アステロイド曲線とその性質

問題

解答・解説

関連記事

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル