こんにちは。今回は連比(比合わせ)についてです。それではどうぞ。
相似をやっていて, こういう類の問題に出くわすことがあります。
例えば次の問題
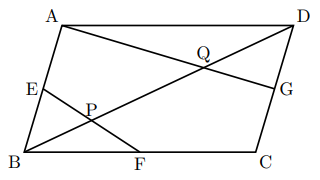
下の平行四辺形ABCDで, 辺AB, BC, CDの中点をそれぞれ, E, F, Gとし, 対角線BDとEF, AGとの交点をそれぞれP, Qとする。このとき, 次の問いに答えなさい。
(1) 線分PQは線分BDの何倍か求めなさい。
(2) ![]() の面積は平行四辺形ABCDの面積の何倍か求めなさい。
の面積は平行四辺形ABCDの面積の何倍か求めなさい。
この問題では![]() ,
, ![]()
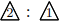 となっており,
となっており, ![]() ,
, ![]() で両者とも同じ線分を分けているが, 比の合計
で両者とも同じ線分を分けているが, 比の合計![]() と
と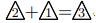 と
と![]() と
と と合計は異なる。これでは比べようがないので,
と合計は異なる。これでは比べようがないので, ![]() と
と の最小公倍数
の最小公倍数 でそろえることにする。
でそろえることにする。
すると, ![]() は3倍,
は3倍,  は4倍することになるので, 下の線分のようになる。
は4倍することになるので, 下の線分のようになる。
これで, ![]() とわかる。
とわかる。
問題の(1)はPQ![]() (倍)
(倍)
(2)は平行四辺形の全体の面積を![]() とすると,
とすると, ![]()
よって![]() 倍とわかる。
倍とわかる。
前途したテクニックは, あくまで比を使って解いた場合で, 分数が好きなら分数を使って簡単に処理できる。それを紹介しておく。こちらの方がスマートなときもある。
![]() ,
, ![]() より,
より, ![]()
として(1)の解を得ることが可能。したがって分数表示で, ![]() を表すと
を表すと![]()
となり, これを整数比で表すと, 上と同じ![]() を得る。
を得る。
このように連比(比合わせ)のテクニックは, ちょっとした応用問題を解くカギになるので, 少なくともどちらか一方のテクニックは習得しておきたいですね。
 数樂管理人のブログ
数樂管理人のブログ