こんにちは。![]() の変化の割合についてです。それではどうぞ。
の変化の割合についてです。それではどうぞ。
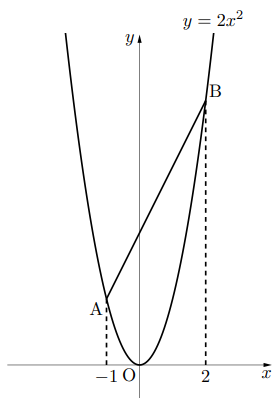
【EX】関数![]() のグラフにおいて,
のグラフにおいて, ![]() の値が
の値が![]() から2まで増加するときの変化の割合を求めなさい。
から2まで増加するときの変化の割合を求めなさい。
この問題は, 中学2年生で学んだ変化の割合の考え方と全く同じである。
それは次の![]() の式である。
の式である。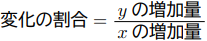
![]()
ここでは, ![]() のとき
のとき![]() ,
, ![]() のとき
のとき![]() であるから,
であるから,
変化の割合![]() (答)
(答)
と求めることが可能。これで, ずっと押し通してもよい。
ただ, 関数![]() においては,
においては, ![]() の値が
の値が![]() から
から![]() まで変化するときの変化の割合は
まで変化するときの変化の割合は
変化の割合![]()
という公式で得られる。公式を使うと
変化の割合![]() (答)
(答)
となる。
また, 次のような問題にもこの公式は威力を発揮する。
【EX】関数![]() において,
において, ![]() の値が2から3まで増加するときの変化の割合と, 一次関数
の値が2から3まで増加するときの変化の割合と, 一次関数![]() の変化の割合が等しいとき,
の変化の割合が等しいとき, ![]() の値を求めなさい。
の値を求めなさい。
この問題で, 公式を用いると![]() の変化の割合は
の変化の割合は![]()
これが, 一次関数の変化の割合である2と等しいので,![]()
となり, ![]() (答)が得られる。
(答)が得られる。
もちろん, ![]() の式を用いても解ける。この内容は, 関数
の式を用いても解ける。この内容は, 関数![]() のところでよく聞かれる問題なので, 公式の理解をきちんとして, 問題に解きなれておく必要がある。この公式は必ずしも覚えておく必要はないが, 知っておくと問題が素早く解くことができ, 何かと便利である。
のところでよく聞かれる問題なので, 公式の理解をきちんとして, 問題に解きなれておく必要がある。この公式は必ずしも覚えておく必要はないが, 知っておくと問題が素早く解くことができ, 何かと便利である。
公式の証明を知りたい方は, 研究テーマにある変化の割合をご覧いただきたい。
最初の問題でグラフの2点A, Bを直線で結ぶと1次関数の式ができると思う。その直線の式の傾きがまさに, 変化の割合の2である。この事実は知っておいて使いこなせれば非常に便利だが, この知識も知らなくても解ける問題がほとんどなので, 余力のある人は覚えておくといいでしょう。これが派生すると, ![]() 上の2点を通る直線の式の公式が得られる。もちろんこれも知らなくてもいいレベルではありますが。
上の2点を通る直線の式の公式が得られる。もちろんこれも知らなくてもいいレベルではありますが。
ではでは。
 中学数学:研究:変化の割合についての考察
中学数学:研究:変化の割合についての考察
 中学数学:攻略法:一次関数のyの増加量について
中学数学:攻略法:一次関数のyの増加量について
 数樂管理人のブログ
数樂管理人のブログ