こんにちは。一次関数の![]() の増加量についてです。それではどうぞ。
の増加量についてです。それではどうぞ。
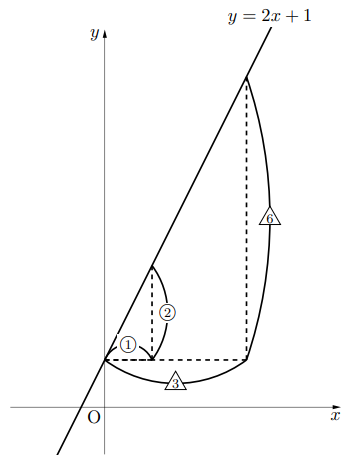
下の図のように, 関数![]() のグラフがある。
のグラフがある。
変化の割合は2であることはご存知のことと思う。
ちなみに変化の割合とは, 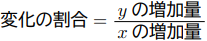
で表される。
この場合変化の割合2というのは, ![]() の増加量が1のときの
の増加量が1のときの![]() の増加量を表すことになります。
の増加量を表すことになります。
上の図でいう![]() が
が![]() の増加量で,
の増加量で, ![]() が
が![]() の増加量になります。結果,
の増加量になります。結果,
変化の割合![]() となります。
となります。
では, ![]() の増加量が
の増加量が (
(![]() の3倍)になったら,
の3倍)になったら, ![]() の増加量はどうなりますか。
の増加量はどうなりますか。
という問いに対して,
代表的なミスとして, ![]() として7と答えるのが誤答の代表的なものです。
として7と答えるのが誤答の代表的なものです。
では何がいけないのか。考えてみましょう。
それは, 変化の割合が2ではなくなっています。この場合,
変化の割合![]()
考えてみると, 一次関数は直線のグラフになります。これは変化の割合がどこをとっても一定ということを表しています。変化の割合が一定でなければ, グラフは折れ曲がってしまいます。
したがって, この一次関数では, どこをとっても![]() が1増加したら
が1増加したら![]() が2増加することになります。よって,
が2増加することになります。よって, ![]() の増加量が
の増加量が![]()
 になったら,
になったら,
同時に![]() の増加量も
の増加量も![]()
 になるわけです。
になるわけです。
小学生の図形で言えば, 拡大縮小の関係になっています。
これによって直線(変化の割合が一定)であることが見えてきます。
結果,
変化の割合![]()
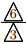
![]() で一定となります。
で一定となります。
この結果から得られる公式として,
(![]() の増加量)=(変化の割合)
の増加量)=(変化の割合)![]() (
(![]() の増加量)
の増加量)
が得られます。変化の割合の式を変形しても得られますが, それはそれとして。
変化の割合が異なるというのは曲線や折れ線グラフなんかは場所によって変化の割合は異なってきます。
ではでは。
 中学数学:研究:変化の割合についての考察
中学数学:研究:変化の割合についての考察
 中学数学:攻略法:y=ax²の変化の割合
中学数学:攻略法:y=ax²の変化の割合 数樂管理人のブログ
数樂管理人のブログ