こんにちは。今回は変化の割合について考察してみようと思います。
変化の割合は2点間の傾きを表す。この割合がどこをとっても一定の場合, グラフは直線を描く。
一次関数![]() とし,
とし, ![]() の変域を
の変域を![]() として, 変化の割合が一定であることを示す。
として, 変化の割合が一定であることを示す。![]() のとき,
のとき, ![]()
![]() のとき,
のとき, ![]()
この2点![]() の傾きは,
の傾きは,  を使って, 次のようになる。
を使って, 次のようになる。![]()
![]() は
は![]() の変域
の変域![]() に関係なく一定でその値は
に関係なく一定でその値は![]() になる。従って一次関数
になる。従って一次関数![]() は直線になる。
は直線になる。
二次関数の変化の割合を次の調べてみる。
二次関数を![]() として, 先と同様,
として, 先と同様, ![]() の変域を
の変域を![]() とする。
とする。![]() のとき,
のとき, ![]()
![]() のとき,
のとき, ![]()
この2点間の傾きは, 先と同様にすると, 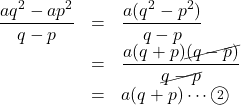
![]() は
は![]() の変域の値
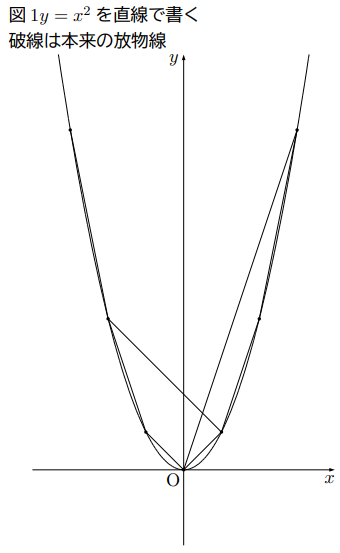
の変域の値![]() によって変わる値で, 常に一定ではない。常に一定でないということは, グラフは曲線を描く, これが放物線になるのである。図1に関数
によって変わる値で, 常に一定ではない。常に一定でないということは, グラフは曲線を描く, これが放物線になるのである。図1に関数![]() で,
で, ![]() が
が![]() の整数をとって直線で結んでみた。また
の整数をとって直線で結んでみた。また![]() ,
, ![]() の傾き,
の傾き, ![]() ,
, ![]() の傾きを線分で表してみた。
の傾きを線分で表してみた。
最後に変化の割合を![]() で調べてみる。
で調べてみる。![]() の変域は同じく
の変域は同じく![]() とする。
とする。![]() のとき,
のとき, ![]()
![]() のとき,
のとき, ![]()
同様にして, 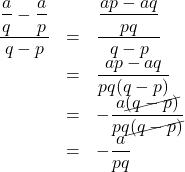
これも二次関数同様, ![]() の変域の値
の変域の値![]() によって変わる値で, 常に一定でない。このことは反比例の式もまた曲線を描くことを意味する。これが双曲線といわれる曲線である。
によって変わる値で, 常に一定でない。このことは反比例の式もまた曲線を描くことを意味する。これが双曲線といわれる曲線である。
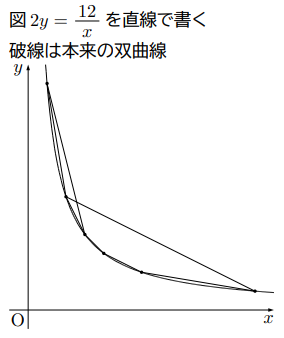
図2に反比例![]() の正の部分を
の正の部分を![]() ともに自然数の座標をとってそれを直線で結んでみた。また,
ともに自然数の座標をとってそれを直線で結んでみた。また, ![]() ,
, ![]() の傾き,
の傾き, ![]() ,
, ![]() の傾きを線分で表してみた。
の傾きを線分で表してみた。
変化の割合って傾きを表すんですよ。だから, これまでで言うと, 2点P, Qを結んだ直線の傾きを表す。これを知っておくと便利ですが, 知らなくても大丈夫なように問題ができていることが多いので, まぁ余力のある人は知識として覚えておくといいでしょう。
 中学数学:攻略法:y=ax²の変化の割合
中学数学:攻略法:y=ax²の変化の割合
 中学数学:攻略法:一次関数のyの増加量について
中学数学:攻略法:一次関数のyの増加量について
 数樂管理人のブログ
数樂管理人のブログ