こんにちは。有名問題をどうぞ。
![]() ,
, ![]() ,
, ![]() ,
, ![]() と無限に続けていくと, 折れ線の端はどんな点に近づいていくか。その点の座標を求めよ。
と無限に続けていくと, 折れ線の端はどんな点に近づいていくか。その点の座標を求めよ。
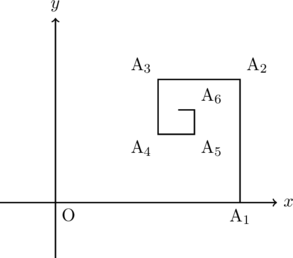
【神奈川大】
【解答】![]()
【解説】![]() 座標は,
座標は, ![]()
これは, ![]()
と書けるので, 和を無視した一般項は, 初項1, 公比![]() の等比数列。つまり,
の等比数列。つまり, ![]() となる。
となる。
したがって, その無限級数和は, ![]()
![]() 座標は,
座標は, ![]()
これは, ![]()
と書けるので, 和を無視した一般項は, 初項![]() , 公比
, 公比![]() の等比数列。つまり,
の等比数列。つまり, ![]() となる。
となる。
したがって, その無限級数和は, ![]()
以上より, 求める座標は, ![]() である。
である。
 数樂管理人のブログ
数樂管理人のブログ 


