こんにちは。相城です。神奈川県から反比例の問題です。日常をテーマとした問題が多くなってきてますので, 歯車とかの問題も復活してきそうですね?それではどうぞ。
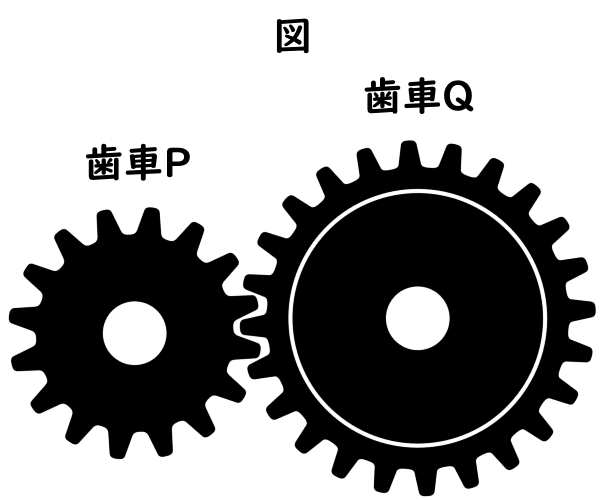
図のように, かみあってそれぞれ回転する歯車Pと歯車Qがある。歯数が24である歯車Pを1秒間に6回転させるとき, 歯車Qの1秒間に回転する数が, その歯数によってどう変わるかを考える。
Aさんは, 歯車Qの1秒間に回転する数について, 次のようにまとめた。![]() にあてはまる数を,
にあてはまる数を, ![]() にあてはまる式を, それぞれ書きなさい。
にあてはまる式を, それぞれ書きなさい。
【まとめ】
歯車Qの歯数が48のとき, 歯車Qは1秒間に3回転する。
また, 歯車Qの歯数が36のとき, 歯車Qは1秒間に![]() 回転する。
回転する。
これらのことから, 歯車Qの歯数を![]() とするとき, 歯車Qの1秒間に回転する数を
とするとき, 歯車Qの1秒間に回転する数を![]() として,
として, ![]() を
を![]() の式で表すと,
の式で表すと, ![]()
となる。

答え
歯車がかみ合っているということは, お互いに動くはの数が等しいということを意味しています。
したがって, Pの歯数が24で回転数が1秒間に6回ということは,
Pの1秒間に動く歯の数は24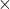 6
6 144
144
このとき歯車Qも144動くので, 歯数が36のときは,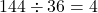
3回転します。
このことから歯車Pと歯車Qの間の関係は
(歯車Pの歯数)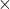 (歯車Pの回転数)
(歯車Pの回転数) (歯車Qの歯数)
(歯車Qの歯数)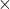 (歯車Qの回転数)となり,
(歯車Qの回転数)となり,
これが成り立つので
144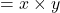
よって求める式は
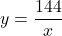
したがって, Pの歯数が24で回転数が1秒間に6回ということは,
Pの1秒間に動く歯の数は24
このとき歯車Qも144動くので, 歯数が36のときは,
3回転します。
このことから歯車Pと歯車Qの間の関係は
(歯車Pの歯数)
これが成り立つので
144
よって求める式は
 数樂管理人のブログ
数樂管理人のブログ 


iは●なのではないでしょうか?
そうですね。訂正しておきました。
ご指摘ありがとうございます。
解答は伏せさせていただきました。